TSPLIB 95

TSPLIB 是一个包含来自不同来源和类型的旅行商问题（TSP）及相关问题样本实例的库。以下问题类别的实例可供使用。

对称旅行商问题（TSP） 给定一组包含n个节点的集合以及每对节点之间的距离，找出一条总长度最小的回路，要求每个节点恰好访问一次。从节点i到节点j的距离与从节点j到节点i的距离相同。

哈密顿回路问题（HCP） 给定一个图，判断该图中是否存在哈密顿回路。

非对称旅行商问题（ATSP） 给定一组包含n个节点的集合以及每对节点之间的距离，找出一条总长度最小的回路，要求每个节点恰好访问一次。在这种情况下，从节点i到节点j的距离与从节点j到节点i的距离可能不同。

顺序排序问题（SOP） 该问题是一个带有额外约束的非对称旅行商问题。给定一组包含n个节点的集合以及每对节点之间的距离，找出一条从节点1到节点n的最短哈密顿路径，同时考虑给定的优先约束。每个优先约束要求某些节点i必须在其他节点j之前被访问。

带容量约束的车辆路径问题（CVRP） 给定n-1个节点、一个仓库以及从节点到仓库和节点之间的距离。所有节点的需求都可以由仓库满足。为了向节点送货，有相同容量的卡车可供使用。问题是找出总长度最小的卡车路线，以满足节点需求而不违反卡车容量约束。卡车的数量未指定。每条路线访问节点的子集，并以仓库为起点和终点。（备注：在某些数据文件中，给出了多个备选仓库。选择一个仓库即可确定一个CVRP。）

除了哈密顿回路问题外，所有问题都在完全图上定义，并且目前所有距离都是整数。可以要求在问题的解决方案中包含某些边。

1. 文件格式

每个文件由说明部分和数据部分组成。说明部分包含有关文件格式和内容的信息。数据部分包含具体数据。

1.1 说明部分

本节中的所有条目均采用 <keyword> : <value> 的形式，其中 <keyword> 表示字母数字关键字，<value> 表示字母数字数据或数值数据。术语 <string>、<integer> 和 <real> 分别表示字符串、整数或实数数据。在数据文件中，关键字的说明顺序（原则上）是任意的，但必须保持一致，即每当指定一个关键字时，都必须知道正确解释该关键字所需的所有必要信息。下面我们列出了所有可用的关键字。

1.1.1 NAME : <string>

标识数据文件。

1.1.2 TYPE : <string>

指定数据的类型。可能的类型有：

• TSP：对称旅行商问题的数据

• ATSP：非对称旅行商问题的数据

• SOPData：顺序排序问题的数据

• HCP：哈密顿回路问题的数据

• CVRP：带容量约束的车辆路径问题的数据

• TOUR：路线的集合

1.1.3 COMMENT : <string>

附加注释（通常在这里给出问题实例的贡献者或创建者的姓名）。

1.1.4 DIMENSION : <integer>

对于TSP或ATSP，维度是指其节点的数量。对于CVRP，它是指节点和仓库的总数。对于TOUR文件，它是指相应问题的维度。

1.1.5 CAPACITY : <integer>

在CVRP中指定卡车的容量。

1.1.6 EDGE WEIGHT TYPE : <string>

指定边权重（或距离）的给定方式。值包括：

• EXPLICIT：在相应部分中明确列出权重

• EUC_2D：二维空间中的欧几里得距离

• EUC_3D：三维空间中的欧几里得距离

• MAX_2D：二维空间中的最大距离

• MAX_3D：三维空间中的最大距离

• MAN_2D：二维空间中的曼哈顿距离

• MAN_3D：三维空间中的曼哈顿距离

• CEIL_2D：二维空间中的欧几里得距离向上取整

• GEO：地理距离

• ATT：针对att48和att532问题的特殊距离函数

• XRAY1：针对晶体学问题的特殊距离函数（版本1）

• XRAY2：针对晶体学问题的特殊距离函数（版本2）

• SPECIAL：在其他地方有记录的特殊距离函数

1.1.7 EDGE WEIGHT FORMAT : <string>

如果边权重是明确给出的，则该字段描述边权重的格式。可选值包括：

• FUNCTION：权重由函数给出（见上文）

• FULL MATRIX：权重由一个完整的矩阵给出

• UPPER_ROW：上三角矩阵（按行，不包括对角线元素）

• LOWER_ROW：下三角矩阵（按行，不包括对角线元素）

• UPPER_DIAG_ROW：上三角矩阵（按行，包括对角线元素）

• LOWER_DIAG_ROW：下三角矩阵（按行，包括对角线元素）

• UPPER_COL：上三角矩阵（按列，不包括对角线元素）

• LOWER_COL：下三角矩阵（按列，不包括对角线元素）

• UPPER_DIAG_COL：上三角矩阵（按列，包括对角线元素）

• LOWER_DIAG_COL：下三角矩阵（按列，包括对角线元素）

1.1.8 EDGE DATA FORMAT : <string>

如果图不是完全图，则该字段描述图中边的给定格式。可选值包括：

EDGE LIST：图由边列表给出 ADJ LIST：图由邻接列表给出

1.1.9 NODE COORD TYPE : <string>

该字段指定是否每个节点都与坐标相关联（例如，坐标可用于图形显示或距离计算）。可选值包括：

• TWOD COORDS：节点由二维坐标指定

• THREED COORDS：节点由三维坐标指定

• NO COORDS：节点没有相关联的坐标

默认值为NO COORDS。

1.1.10 DISPLAY DATA TYPE : <string>

该字段指定如何获得节点的图形显示。可选值包括：

• COORD DISPLAY：根据节点坐标生成显示

• TWOD DISPLAY：给出明确的二维坐标

• NO DISPLAY：无法进行图形显示

如果指定了节点坐标，则默认值为COORD DISPLAY；否则为NO DISPLAY。

1.1.11 EOF :

表示输入数据的结束。此条目是可选的。

1.2 数据部分

根据所选规范，可能需要一些附加数据。这些数据在规范部分之后的相应数据部分中给出。每个数据部分都以相应的关键字开始。部分的长度要么从格式规范中隐式得知，要么由适当的节尾标识符终止。

1.2.1 节点坐标部分（NODE COORD SECTION）:

本部分提供节点坐标。每行的格式为 <整数> <实数> <实数>

如果节点坐标类型为二维坐标（TWOD COORDS），或者 <整数> <实数> <实数> <实数>

如果节点坐标类型为三维坐标（THREED COORDS）。整数表示相应节点的编号。实数表示相关联的坐标。

1.2.2 仓库部分（DEPOT SECTION）:

包含可能的替代仓库节点列表。该列表以-1终止。

1.2.3 需求部分（DEMAND SECTION）:

容量受限的车辆路径问题（CVRP）中所有节点的需求以每行一个的形式给出 <整数> <整数>

第一个整数指定节点编号，第二个整数表示其需求。仓库节点也必须出现在此部分中，但它们的需求为0。

1.2.4 边数据部分（EDGE DATA SECTION）:

图的边在边数据格式（EDGE DATA FORMAT）条目中允许的两种格式之一中指定。如果类型为边列表（EDGE LIST），则边以一系列如下形式的行给出 <整数> <整数>

每个条目给出某条边的终端节点。列表以-1终止。如果类型为邻接列表（ADJ LIST），则该部分由节点的邻接列表列表组成。 节点x的邻接列表指定为 <整数> <整数> ... <整数> -1

其中第一个整数给出节点x的编号，接下来的整数（以-1终止）是与x相邻的节点的编号。邻接列表列表以额外的-1终止。

1.2.5 固定边部分（FIXED EDGES SECTION）:

本部分列出了在问题的每个解决方案中都必须出现的边。要固定的边以每行一个的形式给出，格式为 <整数> <整数>

这意味着从第一个节点到第二个节点的边（弧）必须包含在解决方案中。本部分以-1终止。

1.2.6 显示数据部分（DISPLAY DATA SECTION）:

如果显示数据类型（DISPLAY DATA TYPE）为二维显示（TWOD DISPLAY），则生成显示所需的二维坐标以每行一个的形式给出，格式为 <整数> <实数> <实数>

整数指定相应的节点，实数给出相关联的坐标。

1.2.7 路径部分（TOUR_SECTION）:

本部分指定了一组路径。每个路径由一组整数给出，这些整数表示在该路径中访问节点的顺序。每个这样的路径都以-1终止。额外的-1终止本部分。

1.2.8 边权重部分（EDGE_WEIGHT_SECTION）:

边权重以边权重格式（EDGE WEIGHT FORMAT）条目中指定的格式给出。目前，所有显式数据都是整数，并以其中一种（自解释的）矩阵格式给出，其长度是隐式已知的。

2. 距离函数

对于边权重类型（EGDE WEIGHT TYPE）的各种选择，我们现在描述相应距离的计算方法。在每种情况下，我们都给出了一个（简化的）C语言实现，用于根据输入坐标计算距离。所有涉及浮点数的计算都以双精度算术进行。整数假定以32位字表示。由于距离需要是整数，因此我们将其四舍五入到最近的整数（在大多数情况下）。以下我们使用了四舍五入函数“nint”（“nint(x)”可以用“(int) (x+0.5)”替换）。

2.1 欧几里得距离（L2范数）

对于边权重类型为二维欧几里得（EUC 2D）和三维欧几里得（EUC 3D）的情况，必须为每个节点指定浮点坐标。设x[i]、y[i]和z[i]为节点i的坐标。

在二维情况下，两点i和j之间的距离计算如下：

xd = x[i] - x[j];
yd = y[i] - y[j];
dij = nint(sqrt(xd*xd + yd*yd));

在三维情况下，我们有：

xd = x[i] - x[j];
yd = y[i] - y[j];
zd = z[i] - z[j];
dij = nint(sqrt(xd*xd + yd*yd + zd*zd));

其中，sqrt是C语言中的平方根函数。

2.2 曼哈顿距离（L1范数）

如果边权重类型为二维曼哈顿（MAN_2D）或三维曼哈顿（MAN_3D），则距离以曼哈顿距离给出。

它们计算如下。

二维情况：

xd = abs(x[i] - x[j]);
yd = abs(y[i] - y[j]);
dij = nint(xd + yd);

三维情况：

xd = abs(x[i] - x[j]);
yd = abs(y[i] - y[j]);
zd = abs(z[i] - z[j]);
dij = nint(xd + yd + zd);

2.3 最大距离（L_∞范数）

如果边权重类型为二维最大（MAX_2D）或三维最大（MAX_3D），则计算最大距离。

二维情况：

// 注意：原代码中这一行是重复的，应删除一行
xd = abs(x[i] - x[j]);
yd = abs(y[i] - y[j]);
dij = max(nint(xd), nint(yd));

三维情况：

xd = abs(x[i] - x[j]);
yd = abs(y[i] - y[j]);
zd = abs(z[i] - z[j]);
dij = max(nint(xd), nint(yd), nint(zd));

2.4 地理距离

如果旅行推销员问题是一个地理问题，那么节点对应于点，两点之间的距离是它们在半径为 6378.388 千米的理想化球面上的距离。节点坐标给出了地球上相应点的地理经纬度。纬度和经度的形式为 DDD.MM，其中 DDD 为度，MM 为分。正纬度表示 “北”，负纬度表示 “南”。正经度表示 “东”，负纬度表示 “西”。例如，奥格斯堡的输入坐标为 48.23 和 10.53，即北纬 48 度 23 分，东经 10 度 53 分。

设x[i]和y[i]为城市i在上述格式中的坐标。首先将输入转换为以弧度给出的地理纬度和经度。

PI = 3.141592;
deg = nint(x[i]);
min = x[i] - deg;
latitude[i] = PI * (deg + 5.0 * min / 3.0) / 180.0;
deg = nint(y[i]);
min = y[i] - deg;
longitude[i] = PI * (deg + 5.0 * min / 3.0) / 180.0;

然后，两个不同节点i和j之间的距离（以千米为单位）计算如下：

RRR = 6378.388;
q1 = cos( longitude[i] - longitude[j] );
q2 = cos( latitude[i] - latitude[j] );
q3 = cos( latitude[i] + latitude[j] );
dij = (int) ( RRR * acos( 0.5*((1.0+q1)*q2 - (1.0-q1)*q3) ) + 1.0);

函数“acos”是余弦函数的反函数。

2.5 伪欧几里得距离

边权重类型ATT对应于一种特殊的“伪欧几里得”距离函数。设x[i]和y[i]为节点i的坐标。两点i和j之间的距离计算如下：

xd = x[i] - x[j];
yd = y[i] - y[j];
rij = sqrt((xd*xd + yd*yd) / 10.0);
tij = nint(rij);
if (tij < rij) dij = tij + 1;
else dij = tij;

2.6 欧几里得距离的上限

边权重类型CEIL 2D要求将二维欧几里得距离向上取整到下一个整数。

2.7 晶体学问题的距离

我们已将如[1]中所述的晶体学问题纳入TSPLIB中。这些问题并未明确给出，但提供了子程序来生成该参考文献中提到的12个问题及其子问题（见第3.2节）。

为了计算这些问题的距离，必须考虑三个电机的移动。有两种类型的距离函数：一种假设电机速度相等（XRAY1），另一种使用不同的速度（XRAY2）。相应的距离函数在分发文件中以FORTRAN实现（文件deq.f和duneq.f）。

为了获得整数距离，我们建议将原始子程序计算的距离乘以100.0并四舍五入到最近的整数。

以下是我们为电机速度相等情况下在FORTRAN版本中修改的距离函数列表。

    INTEGER FUNCTION ICOST(V,W)
    INTEGER V,W
    DOUBLE PRECISION DMIN1,DMAX1,DABS
    DOUBLE PRECISION DISTP,DISTC,DISTT,COST 
    DISTP=DMIN1(DABS(PHI(V)-PHI(W)),DABS(DABS(PHI(V)-PHI(W))-360.0E+0)) 
    DISTC=DABS(CHI(V)-CHI(W))
    DISTT=DABS(TWOTH(V)-TWOTH(W))
    COST=DMAX1(DISTP/1.00E+0,DISTC/1.0E+0,DISTT/1.00E+0)
C *** Make integral distances ***
    ICOST=AINT(100.0E+0*COST+0.5E+0)
    RETURN
    END

数字PHI(), CHI(), 和 TWOTH() 分别代表在生成的旅行商问题中点的x、y、z坐标。请注意，TSPLIB95仅包含原始的距离计算方法，没有上述修改。

2.8 验证

为了验证距离函数实现的正确性，我们给出了某些“标准”巡回路线1, 2, 3, ..., n的长度。

对于pcb442、gr666和att532的标准巡回路线长度分别为221,440、423,710和309,636。

对于问题xray14012（在[21]中考虑的第8个问题），使用XRAY1距离得出的标准巡回路线长度为15,429,219，而使用XRAY2距离得出的长度为12,943,294。

3. 库文件描述

在本节中，我们列出了当前可用的所有问题实例，以及关于最优巡回路线长度（如果已知）或其下界和上界的信息。

3.1 对称旅行商问题

旅行商问题实例包含在tsp目录中。表1给出了问题名称、城市数量、问题类型以及已知的最优巡回路线长度的下界和上界（单个数字表示已知最优长度）。条目MATRIX表示数据以1.1.7中的某一种矩阵格式给出。相应数据文件的名称是通过在问题名称后添加后缀“.tsp”获得的。还提供了一些最优巡回路线，对应的文件名以“.opt.tour”为后缀。

Table 1 Symmetric traveling salesman problems (Part I)

Table 1 Symmetric traveling salesman problems (Part II)

晶体学问题

在tsp目录下的xray.problems文件中，我们发布了由Bland和Shallcross编写的程序以及生成[1]中讨论的晶体学问题所需的数据。xray.problems文件是一个将后续提到的单个文件合并而成的文件。这些单个文件需要使用编辑器从xray.problems文件中提取。以下提供了原始文件：

read.me、deq.f、duneq.f、daux.f、gentsp.f
a.data、b.data、d.data、e.data、f.data

此外，我们还包含了特别准备的数据文件，用于生成[1]中提到的12个问题。这些文件的命名从xray1.data到xray12.data。使用这些数据文件和gentsp.f程序，可以生成12个对称旅行商问题（TSP）。我们建议将这些问题实例分别命名为xray4472、xray2950、xray7008、xray2762、xray6922、xray9070、xray5888、xray14012、xray5520、xray13804、xray14464和xray13590。

为了验证生成程序的正确使用，我们列出了xray14012.tsp文件的部分内容。

• NAME: xray14012

• COMMENT: 晶体学问题8（Bland/Shallcross）

• TYPE: TSP

• DIMENSION: 14012

• EDGE_WEIGHT TYPE: XRAY2

• NODE_COORD_SECTION（节点坐标部分）: （此处列出了从1到14012的节点坐标，以三个维度表示，例如）: 1 -91.802854544029 -6.4097888697337 176.39830490027 ... 14012 88.197145450242 6.4097888697337 176.39830490027

3.2 哈密顿回路问题

哈密顿回路问题的实例包含在hcp目录中。目前，我们有以下数据文件：

alb1000.hcp、alb3000b.hcp、alb3000e.hcp、alb2000.hcp、alb3000c.hcp
alb4000.hcp、alb3000a.hcp、alb3000d.hcp、alb5000.hcp

每个实例都包含一个哈密顿回路，该回路在相应的.opt.tour文件中给出。在alb4000问题实例中，有两个边是固定的。

除了这些文件外，该目录还包含了M. Jünger和G. Rinaldi编写的C程序tspleap.c。该程序可用于生成TSPLIB格式的TSP实例，这些实例源自以下问题：判断一个(r,s)跳跃者能否在mxn国际象棋棋盘上从某个方格开始，恰好访问每个方格一次，并返回起始方格。tspleap.c文件中提供了详细的文档说明。

3.3 非对称旅行商问题

表2列出了非对称旅行商问题（ATSP）的实例（位于atsp目录中）及其最优解值。相应数据文件的名称是通过在问题名称后添加后缀“.atsp”获得的。对于ftv90、ftv100、ftv110、ftv120、ftv130、ftv140、ftv150和ftv160这些问题，其数据文件并不存在。这些实例是从ftv170中获得的。例如，ftv120是由ftv170中前121个节点定义的子问题，ftv130是由前131个节点定义的，以此类推。

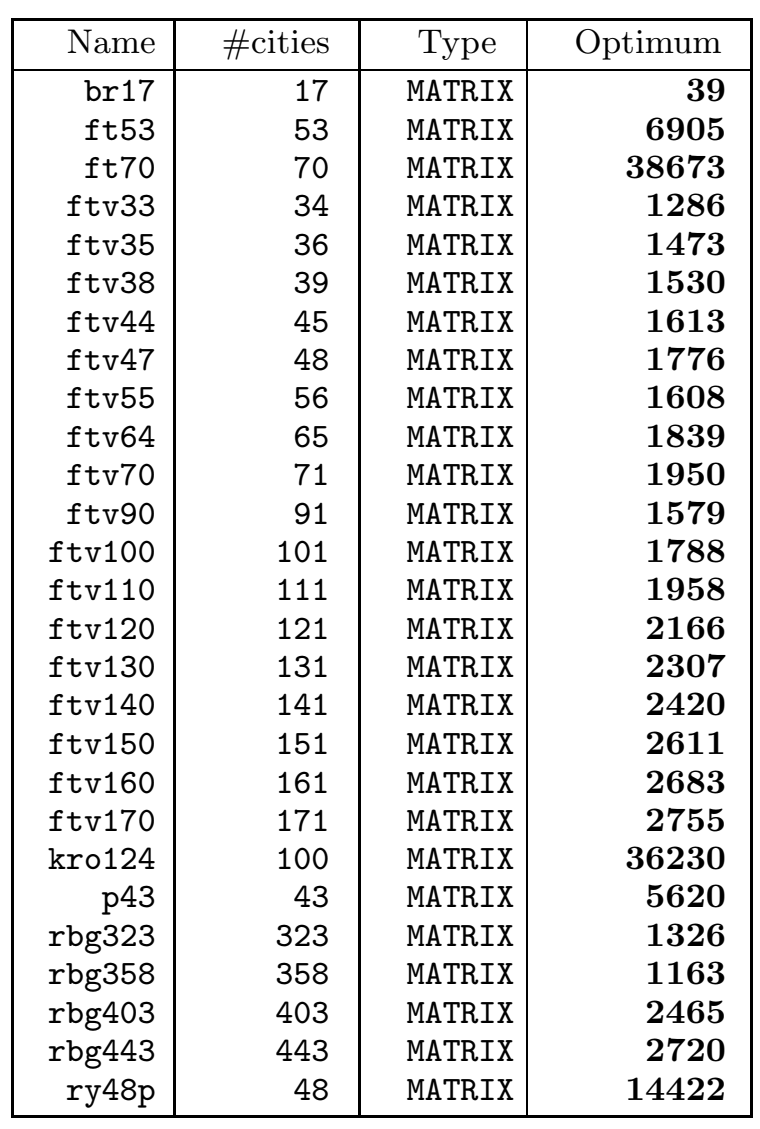
表 2 非对称旅行行商问题

3.4 序列排序问题

序列排序问题的每个实例都由一个完整的矩阵C给出，该矩阵具有以下特性。如果节点i必须在节点j之前，则Cji被设置为-1。假设矩阵C在优先关系上是传递闭包的，即如果i必须在j之前，且j必须在k之前，则可以推断出i必须在k之前，因此也必须将Cki设置为-1。由于我们要求在每个可行路径中，节点1是第一个节点，节点n是最后一个节点，因此序列排序问题（SOP）的实例总是满足：对于所有i=2,...,n，Ci1=-1；对于所有j=1,...,n-1，Cnj=-1。C1n被设置为无穷大。C的所有其他元素都是非负整数值。

表3 序列排序问题

表3列出了序列排序问题（SOP）的实例（位于sop目录中），以及这些实例的最优路径长度的已知下界和上界。相应数据文件的名称是通过在问题名称后添加后缀“.sop”获得的。

3.5 带容量约束的车辆路径问题

带容量约束的车辆路径问题的数据包含在vrp目录中。数据文件的后缀为“.vrp”。目前，我们拥有以下数据文件：

att48.vrp, eil30.vrp, eil7.vrp, eilB76.vrp, eil13.vrp, eil31.vrp, eilA101.vrp, eilC76.vrp, eil22.vrp, eil33.vrp, eilA76.vrp, eilD76.vrp, eil23.vrp, eil51.vrp, eilB101.vrp, gil262.vrp

基于这些数据集，可以定义各种问题，例如，根据车辆数量是否固定等条件，因此我们在这里不列出最优解。一些值已在数据文件中给出。

3.6 其他特殊文件

除了数据和解决方案文件外，库中还包含以下特殊文件：

• TSPLIB VERSION：提供库的当前版本

• README：TSPLIB的简短信息

• DOC.PS：TSPLIB的描述（PostScript格式）

4. 备注

1. lin318问题原本是一个哈密顿路径问题。通过增加额外要求，即路径中包含从1到214的边，即可得到该问题。数据在linhp318.tsp文件中给出。

2. 文献中有些数据集使用了不同的名称。下面我们给出了在[3]和[2]中使用的相应名称。

3. 部分车辆路径问题也有TSP版本。在这种情况下，仓库只是被视为普通节点。gil262问题原本包含两个相同节点，其中一个已被删除。

4. 潜在贡献者应向本库提供格式适当的数据文件，并联系： Gerhard Reinelt 海德堡大学应用数学研究所 德国海德堡，Neuenheimer Feld 294，D-69120 电话：(6221) 56 3171 传真：(6221) 56 5634 电子邮件：Gerhard.Reinelt@IWR.Uni-Heidelberg.DE

5. 我们也欢迎提供有关库中问题的新界限或最优解的信息，以及计算研究的参考文献（将被列入参考文献列表）。