---

标题：A vertex weighting-based double-tabu search algorithm for the classical p-center problem
作者：Qingyun Zhang a, Zhipeng Lü a, Zhouxing Su a, Chumin Li b
论文：https://qiming-pic.oss-cn-wuhan-lr.aliyuncs.com/p-Center-Problem1.pdf

摘要

p-中心问题（The p-center problem）是NP难问题，旨在从一组候选中心中选择p个中心以服务于所有客户，同时最小化每个客户与其分配的中心之间的最大距离。为解决这一具有挑战性的优化问题，我们将p-中心问题转化为一系列决策子问题，并提出了一种基于顶点加权的双禁忌搜索（VWDT）算法。该算法结合了顶点加权策略和一种结合了基于解和基于属性的禁忌策略的双禁忌搜索，以帮助搜索过程跳出局部最优陷阱。对文献中总共510个公开实例的计算实验表明，VWDT算法与最先进的算法相比具有高度竞争力。具体而言，VWDT算法改进了84个大型实例的先前最佳已知结果，并与其他所有实例的最佳结果持平。除了解决方案质量的改进外，VWDT算法在文献中的其他最先进的算法中，尤其是在一些大型实例上，要快得多。此外，我们还进行了额外的实验，以分析VWDT算法中关键组件（如顶点加权和双禁忌搜索策略）的影响。

1. 引言

p-中心问题是一个已被证明为NP难题的优化挑战（Kariv和Hakimi，1979）。它要求从一组候选中心中定位p个中心，来为一组客户提供服务，其中每个客户都寻求其最近的中心之一进行服务。每个客户与其服务提供商之间都存在一个服务弧。p-中心问题的目标是最小化客户与其服务提供商之间的最长服务弧，我们将最长服务弧的长度称为覆盖半径。

𝑝-中心问题广泛存在于实际应用中。例如，它可以构建电信领域中的重要问题，如无线传感器网络优化（Liao和Ting，2018；Zhang等，2021）。在城市规划的背景下，𝑝-中心问题可以构建确定紧急中心（Toregas等，1971）、医院（Hakimi，1964）、银行（Xia等，2010）和充电站（Rigas等，2018）位置的问题，以服务于社区。同样，𝑝-中心问题也可以模拟供应链管理中的生产工厂位置和仓库分布（Amiri，2006）。

禁忌搜索是由Glover（1989）最初提出的一种优化算法。它将禁忌策略融入局部搜索框架中，以跳出局部最优。传统的基于属性的禁忌策略通常记录最近访问的解决方案的有限特征，其性能可能对称为禁忌期限的参数敏感。最近，基于解的禁忌搜索方法引起了广泛关注，并已用于解决许多组合问题，如最小差分分散问题（Wang等，2017）、0-1多维背包问题（Lai等，2018）和最大最小和分散问题（Wang等，2021）。基于解的禁忌策略通过记录访问过的完整解向量，以更系统的方式跟踪搜索轨迹。加权技术是另一种跳出局部最优陷阱的强大技术，它非常灵活且自适应。它类似于引导式局部搜索（Voudouris和Tsang，2003），并已成功应用于许多问题，如集合覆盖问题（Gao等，2015）、最小顶点覆盖问题（Cai等，2011，2013）和可满足性问题（Luo等，2012）。

在本文中，我们提出了一种元启发式算法——基于顶点加权的双禁忌搜索（VWDT）算法，用于解决p-中心问题。VWDT算法结合了顶点加权技术和禁忌搜索，后者融合了基于解和基于属性的禁忌策略。与之前的元启发式算法直接解决原始优化问题不同，VWDT算法通过处理决策版本来解决p-中心问题。具体而言，我们将p-中心问题转化为一系列决策子问题。也就是说，对于每个可能的覆盖半径r，我们检查所有顶点是否都可以被一个位于覆盖半径r内的中心所覆盖。这相当于解决一系列最大覆盖选址子问题（Church和ReVelle，1974）。事实上，通过利用原始问题的下界和上界，子问题的数量会相对较少，并且由于它们彼此独立，我们可以并行解决它们。在包含三组共174个经典基准实例和一组336个p-中心问题的大规模实例上进行测试，VWDT算法在84个实例上改进了已知的最佳结果，并在其余420个实例上达到了记录水平。此外，达到这些结果所需的计算时间远少于文献中最先进的参考算法。

Zhang等人（2020）提出了该算法的一个初步版本，名为VWTS，本文在以下方面对其进行了扩展和改进：

1. 我们采用了一种简化方法来简化实例，并进一步提高了算法的搜索效率。
2. 除了原始的顶点加权技术外，通过结合基于解和基于属性的禁忌策略，我们使用了一种新的混合双禁忌搜索框架来替代原始的简单禁忌策略，从而在强化和多样化之间实现更好的平衡，并防止搜索过程中出现可能的循环。
3. 当存在多个等价的邻近解选择时，我们使用年龄策略来打破平局，更倾向于选择那些长时间未被移入或移出候选解的集合。
4. 我们的新改进算法在文献中使用的超过200,000个顶点的更大实例上进行了测试，而Zhang等人（2020）中的最大实例仅包含3038个顶点。我们的算法能够改进这些大规模实例上84个实例的先前已知最佳结果。
5. 在来自pcb3038的4个困难实例上获得了新的最佳已知结果，并且计算效率也得到了显著提高。
6. 我们进行了额外的实验分析，以展示我们算法关键组件的重要性。

本文概述如下：第2节回顾了与p-中心问题相关的先前研究工作。第3节介绍了p-中心问题的定义和重构。第4节描述了提出的基于顶点加权的双禁忌搜索算法。第5节展示了计算实验，将VWDT算法与文献中的最先进算法进行了比较。第6节分析和比较了算法的一些关键要素，以展示它们如何影响算法的性能。第7节总结了本文，并提出了未来的研究方向。

2. 相关工作

自Hakimi（1964年）提出以来，p-中心问题作为最经典的选址问题之一，在过去50年里引起了学术界的广泛关注，并提出了多种智能优化算法。p-中心问题主要有三种方法：精确算法、近似算法和元启发式算法。

在精确算法方面，解决p-中心问题的一个流行框架是解决一系列最小集合覆盖问题（Daskin, 2013）。Minieka（1970）是首批使用这种方法解决p-中心问题的研究者之一。具体而言，Minieka（1970）提出了一种迭代算法，该算法在每次迭代中解决一个给定半径下的集合覆盖问题，验证是否可以使用不超过p个中心在半径内覆盖所有客户。Daskin（2000）探讨了p-中心问题与集合覆盖问题之间的关系，并利用拉格朗日松弛法解决了后者。Ilhan等人（2002）提出了一种两阶段算法。第一阶段通过迭代判断给定半径下线性规划（LP）公式的可行性，找到最佳可能的下界。第二阶段通过求解一系列整数规划（IP）模型来改进获得的下界，直到IP公式变得可行，即找到一个可行的覆盖半径，使得所有客户都被覆盖。Elloumi等人（2004）为p-中心问题提出了一个新的混合整数规划（MIP）模型和一个用于计算更紧下界的多项式算法。他们还提出了一个扩展问题，称为容错p-中心问题。Calik和Tansel（2013）引入了一种新的整数规划公式和基于分解技术的精确算法来解决p-中心问题，其中所提公式的松弛给出了比Elloumi等人（2004）中更紧的下界。Al-Khedhairi和Salhi（2005）对Ilhan等人（2002）和Daskin（2000）的算法进行了一些修改，以减少搜索过程中的整数线性规划（ILP）迭代次数和需要解决的子问题数量。Contardo等人（2019）提出了一种行生成方法，该方法通过迭代解决p-中心问题的小覆盖子问题。后来，Liu等人（2020）提出了一种通过集合覆盖和可满足性（SAT）来解决p-中心问题的方法，这是第一种基于SAT的p-中心问题求解方法。该方法基于Pullan（2008）提出的PBS算法和Yin等人（2017）提出的GRASP/PR算法得到的先前最佳解决方案，改进了3个大规模实例上的最佳已知结果，并证明了所得解决方案的最优性。Gaar和Sinnl（2022）提出了一种新的整数规划公式，该公式可以通过从p-中心问题的经典公式投影得到，并通过分支切割法求解。Contardo等人（2019）、Liu等人（2020）以及Gaar和Sinnl（2022）提出的算法是解决p-中心问题的最佳精确算法。

除了精确方法外，过去几十年还提出了多种近似算法来解决p-中心问题。Hochbaum和Shmoys（1985）为具有三角形不等式的p-中心问题提出了一个2-近似算法。Martinich（1988）使用顶点关闭方法来解决p-中心问题，并提出了几个定理来验证搜索过程中的最优解。最初，所有中心都是开放的，然后根据p-中心问题的优化目标选择n-p个中心进行关闭。Garcia-Diaz等人（2019）对最具代表性的近似算法进行了分析和实验评估，这些算法包括一些针对p-中心问题的2-近似算法（Sh Shmoys, 1995和Gon Gonzalez, 1985）和3-近似算法（CDS Garcia-Diaz等, 2017）。

元启发式算法是解决组合优化问题的有效方法。在过去几十年里，已经提出了许多用于解决p-中心问题的元启发式算法。Mladenović等人（2003）为p-中心问题提出了变邻域搜索（VNS）、多起点局部搜索和链替换禁忌搜索元启发式算法。他们在OR-Library的40个p-中位（Mladenović等, 2007）实例和TSPLIB中最多包含3038个顶点的98个实例上进行了实验。Caruso等人（2003）提出了一种名为Dominant的元启发式算法，通过预定义的覆盖半径解决一系列集合覆盖问题。Robič和Mihelič（2005）为最小支配集问题引入了一种多项式时间启发式算法，该算法使用所谓的评分技术来解决顶点受限的p-中心问题。Pullan（2008）提出了一种名为PBS的模因算法，这是一种基于局部搜索过程的基于种群的元启发式算法。通过使用表型交叉和有向变异算子，生成了一组精英初始解，并通过局部搜索算法将解改进到局部最优。Salhi和Al-Khedhairi（2010）设计了一种三级元启发式算法，该算法将VNS与扰动方案相结合，并将其集成到如Daskin（2000）的精确算法中来解决p-中心问题。Irawan等人（2016）介绍了一种包含两个元启发式算法的三阶段方法，该方法结合了VNS、精确方法和聚合技术来解决大型p-中心问题。Yin等人（2017）为p-中心问题提出了一种GRASP/PR算法，该算法将路径重连与贪婪随机自适应搜索过程（GRASP）相结合。它改进了10个大规模实例上的先前最佳已知结果。Ferone等人（2017）提出了一种基于关键顶点概念的新智能局部搜索算法，称为GRASP+plateau-surfer，并将其嵌入到GRASP框架中。Zhang等人（2020）提出了一种基于顶点加权的禁忌搜索算法，这是解决p-中心问题的最佳元启发式算法。

3. 问题描述

𝑝-中心问题定义在无向完全图 G=(V,E) 上，其中 V=\{1,2,\ldots,n\} 是顶点集，𝐸 是边集。每对顶点 𝑖 和 𝑗 之间的距离为 d_{ij}\in\mathbb{R}^{+}。每个顶点 𝑖 ∈ 𝑉 对应一个客户，该客户需要从 𝑝 个中心之一获取服务，这些中心应从候选中心集 𝐶 ⊆ 𝑉 中选择（通常 𝐶 = 𝑉）。解可以定义为 (𝒙, 𝒚, 𝑟)。

具体来说，x=\{x_{j}|j\in C\}，其中 X_{j} 是一个决策变量，当且仅当候选中心 𝑗 ∈ 𝐶 被选为中心时，它等于 1。y=\{y_{ij}|i\in V,j\in C\}，其中 y_{ij} 是一个二元变量，当且仅当顶点 𝑖 ∈ 𝑉 由中心 𝑗 ∈ 𝐶 服务时，y_{ij} = 1。r\in\mathbb{R}^{+} 是最长服务弧的长度，即覆盖半径。基于上述符号，我们可以将 𝑝-中心问题的经典混合整数规划（MIP）模型（Daskin, 2013）表述如下：

在模型（𝑃𝐶）中，目标（1）旨在最小化覆盖半径。约束（2）确保有 𝑝 个中心被打开。约束（3）确保每个顶点必须由且仅由一个中心服务。约束（4）限制只有打开的中心才能为顶点提供服务。约束（5）确保覆盖半径 𝑟 不短于任何服务弧。在最优解中，约束（5）中至少有一个等式成立，否则 𝑟 可以进一步减小。这一事实意味着对于特定的 𝑝-中心实例，最优覆盖半径必须等于某个边 d_{ij} 的长度。因此，对于不同的边长有序列表 R=\{d_{ij}|i\in V,j\in C\}=\{r_1,r_2,\ldots,r_k\}，其中 r_{1}<r_{2}<\cdots<r_{k}，我们寻找最小的秩 𝑞，使得在添加约束 r\leq r_{q} 后，模型（𝑃𝐶）仍然可行，但如果添加约束 r\leq r_{q-1}，则它变得不可行。然后，这样的 r_{q} 是最优覆盖半径。

基于最大覆盖位置问题和 𝑝-中心问题之间的关系，如果我们固定一个实例的边长秩 𝑞，则 𝑝-中心问题等价于最大覆盖位置问题（Church and ReVelle, 1974）。具体来说，对于每个候选中心 𝑗 ∈ 𝐶，令 S_{j}^{q}\:=\:\{i\:\in\:V|d_{ji}\:\leq\:r_{q}\:\} 表示在半径 r_{q} 内可以由候选中心 𝑗 服务的顶点集。我们可以得到一个最大覆盖位置问题实例 S^{q}=\{S_{j}^{q}|j\in C\}。然后，如果我们能从 𝑆𝑞 中选择 𝑝 个集合，其并集包含所有顶点，我们可以推导出 𝑟𝑞 是原始 𝑝-中心问题中覆盖半径的上界，反之亦然。因此，如果已知最优边长秩 𝑞，我们可以将模型（𝑃𝐶）重新表述为由等式（7）–（10）定义的最大覆盖位置问题（Daskin, 2000; Ilhan et al., 2002），其中模型（𝑀𝐶𝐿𝑞 ）中每个决策变量 x_j 的含义与模型（𝑃𝐶）中对应的变量相同，而 𝑢𝑖 是一个二元变量，当顶点 𝑖 未被任何中心覆盖时，𝑢𝑖 = 1。

在这里，我们采用等价目标来最大化覆盖的顶点数，即最小化未覆盖的顶点数，如目标函数（7）所示。约束（8）保证每个未覆盖的顶点都会被计入目标中。约束（9）确保恰好有 𝑝 个中心被打开。为了找到最优覆盖半径，我们需要遍历不同的边长列表 𝑅，以检查每个可能的覆盖半径。对于每个 r_{q}，我们判断 𝑝-中心问题是否存在可行解，即在半径 r_{q} 内有 𝑝 个集合覆盖所有顶点。我们反复选择下一个 𝑞，直到 r_{q} 无效。然后，r_{q+1} 是原始问题的最佳解。

4. 基于顶点加权的双禁忌搜索

4.1. 总体框架

我们的VWDT（Vertex Weighting-based Double-Tabu，基于顶点加权的双禁忌）算法从一个通过启发式方法（例如，Pullan于2008年提出的PBS方法）在有限时间内获得的模型(𝑃𝐶)的上界𝑟_𝑞开始，然后依次解决模型(MCL_{q-1})、(MCL_{q-2})，……，直到在给定的时间限制内无法找到可行解为止。因此，我们将重点关注名为VWDT𝑞的子程序，该程序用于在给定的半径下求解模型(𝑀𝐶𝐿𝑞)。

算法1给出了VWDT𝑞的主要框架。在初始化向量和变量后（如第1-2行所示），提出的VWDT𝑞算法从一个由构造性启发式算法生成的初始解开始（第3行，见4.2节），并将已打开的中心集合记录在𝑋、𝑋′和𝑋^∗中。然后，VWDT𝑞通过基于顶点加权的双禁忌搜索过程迭代地寻找具有更少未覆盖顶点的更优解（第5-16行）。在每次迭代中，VWDT𝑞首先评估当前解的交换邻域，并记录处于非禁忌状态的最佳邻域移动(𝑖, 𝑗)（第6行）。然后，它执行最佳移动，将顶点𝑖换入当前中心集，并将顶点𝑗换出（第7行）。如果当前解𝑋优于迄今为止找到的最佳解𝑋^∗，则使用𝑋更新最佳解（第8-9行），其中𝑈(𝑋)表示在当前解𝑋中未覆盖的顶点集合。否则，当当前解陷入局部最优时，即函数 FindPair() 返回的最佳移动无法覆盖更多顶点时（第10行），VWDT𝑞将增加每个未覆盖顶点的权重（第11-12行），其中𝛿将在4.4节中介绍。在每次迭代的末尾，将更新禁忌列表和其他数据结构（第14-15行）。最后，一旦达到时间限制或其他用户指定的终止条件，VWDT𝑞将终止并返回最佳解𝑋^∗（第17行）。

4.2. 初始化

初始化包括一个简化过程和初始解的构造。首先，一些中心必须包含在最优解中。如果一个顶点仅由其自身覆盖，则必须选择该顶点来覆盖它。显然，这类顶点可以固定地作为中心，然后我们只需要选择𝑝 − 𝑙个中心，其中𝑙是固定中心的数量。

接下来，VWDT𝑞采用构造性启发式方法来选择𝑝个中心以形成初始解𝑋。设S_{j}表示在当前半径内候选中心𝑗可以服务的顶点集合，我们有U(X)= V\backslash U_{j\in X}S_{j}。相反，我们用C_{i}表示服务顶点𝑖的候选中心集合，即C_{i} = \{ j \in C| i \in S_{j}\}。构造性启发式方法迭代地打开（即将中心插入当前解𝑋中）当前最佳候选中心j^{*}=\arg\max_{j\in C\setminus X}|S_{j}\cap U(X)|，该中心覆盖最多的未覆盖顶点，直到打开𝑝个中心。如果有多个当前最佳候选中心覆盖相同数量的未覆盖顶点，则随机打破平局。观察到每次迭代中选择最佳中心需要𝑂(𝑛)时间，并且总共有𝑝个中心。因此，构造过程的时间复杂度为𝑂(𝑛𝑝)。

4.3. 加权技术

初始解的质量通常较差，因此我们采用基于加权的禁忌搜索来迭代改进由构造性启发式方法获得的解。顶点加权技术的主要思想是通过改变目标函数来帮助搜索跳出局部最优。如式（7）所示，我们采用了一个直观的目标函数，该函数最小化了未覆盖顶点的数量。当引入顶点权重𝑤𝑖时，我们用式（11）替换目标函数𝑓(𝑋)。

因此，VWDT𝑞实际上解决的是由式（8）至（11）组成的模型（SC_{q}^{p}）。请注意，权重𝑤𝑖不是预定义的值，而是随着搜索的进行而变化。如果在搜索过程中某个顶点长时间未被覆盖，则意味着该顶点对于实现完全覆盖至关重要，我们应给予其更高的优先级。具体来说，当禁忌搜索遇到局部最优解𝑋时，VWDT𝑞会将每个未覆盖顶点𝑖 ∈ 𝑈(𝑋)的权重𝑤_𝑖增加1（算法1，第11-13行）。然而，无论权重如何配置，目标函数（11）的最优值始终为零。更新后的权重重塑了解空间的格局，使得𝑋不再是局部最优解。当遇到停滞时，顶点在𝑈(𝑋)中出现的频率越高，其权重就越大。因此，它引导搜索跳出局部最优，并继续探索其他解。

与禁忌策略相比，顶点加权技术以自适应的方式使搜索多样化。一方面，它关注结果而非原因，从而防止未覆盖顶点的出现，而不是像禁忌策略那样禁止打开或关闭中心。另一方面，它以平滑的方式而不是非黑即白的方式修改解空间，即邻域移动变得更好或更差，而不是有效或无效。

请注意，在局部搜索的每次迭代中，当根据加权目标函数式（11）存在多个最佳邻近解时，我们采用基于年龄的策略来打破平局。具体来说，候选中心的年龄表示它在局部搜索过程中最近一次作为中心的迭代次数。如果候选中心从未作为中心打开过，则其年龄为零。候选中心的年龄越小，表示其未被打开的时间越长。因此，我们通过偏爱年龄值较小的邻近解来打破平局。顶点𝑗的年龄表示为𝑎_𝑗。当加权目标函数无法区分相等解时，此策略能够使搜索多样化。

4.4. 邻域结构与评估

为了改进模型（MCL_{q}^{w}）生成的初始解，VWDT𝑞采用了受大多数元启发式算法在解决𝑝-中心问题时所使用的经典邻域结构启发的交换邻域（Pullan, 2008）。然而，在重新构建的模型中，邻域评估以及专用的加速策略都有所不同。具体来说，交换操作Swap(𝑖, 𝑗)通过向中心集合（打开）中添加一个候选中心𝑖 ∈ 𝐶 ⧵𝑋，并从中心集合（关闭）中移除中心𝑗 ∈ 𝑋，来生成一个邻近解X\oplus \text{Swap} (i,j)=X\cup\{i\}\setminus\{j\}。

众所周知，邻域评估是基于局部搜索的元启发式算法中最耗时的步骤。在最佳改进策略下，局部搜索会在每次迭代中评估所有可行的移动，并执行提供最大目标值改进的最佳邻域移动。对于每次迭代中的交换移动邻域评估，时间复杂度为𝑂(𝑝(𝑛 − 𝑝))，因此在大型实例上可能会非常耗时。为了克服性能问题，VWDT𝑞采用了增量评估技术和邻域采样策略。

一方面，为了加速邻域评估过程，VWDT𝑞算法采用增量评估机制，通过存储和维护𝛿𝑗(𝑗 ∈ 𝐶)（如式（12）所示），而不是简单地计算目标函数式（11），来高效地评估所有邻域移动。

其中，\delta_{j}记录了翻转候选中心𝑗的打开状态所带来的结果。具体来说，对于中心𝑗 ∈ 𝑋，\delta_{j}是只被中心𝑗覆盖的顶点的权重之和。对于每个候选中心j\notin X，\delta_{j}是S_{j}中所有未覆盖顶点的权重之和。然后，我们可以在𝑂(1)时间复杂度内增量地评估打开或关闭一个中心的目标值。但是，我们需要在每次打开或关闭一个中心后更新受影响的𝛿值。具体来说，我们可以通过f(X\cup\{i\})=f(X)-\delta_{i}计算每个邻近解的目标值，并更新相关的𝛿值，从而得到f(X\oplus \text{Swap}(i,j))=f(X\cup\{i\})+\delta_j。我们知道，在每次迭代中，典型的禁忌搜索算法会评估许多移动，但只执行其中一个，而单个邻域移动对当前解只带来微小的变化。因此，我们可以从维护和查询缓存中受益，而不是为每个移动都从头开始计算目标函数。

另一方面，已经覆盖的顶点无法再提高目标值，只有当未覆盖的顶点被覆盖时，目标值才能得到提高。因此，VWDT𝑞仅当候选中心𝑗覆盖𝑈(𝑋)中的一些未覆盖顶点时，才会评估交换操作Swap(𝑖, 𝑗)。由于每个顶点最终都需要被覆盖，VWDT𝑞以更紧凑的方式探索邻域，以进一步减小邻域的大小。具体来说，它随机选择一个顶点𝑘 ∈ 𝑈(𝑋)，并仅评估满足𝑖 ∈ C_k和𝑗 ∈ 𝑋的交换操作Swap(𝑖, 𝑗)。这种采样策略不仅减少了邻域评估的时间消耗，还作为副作用提高了搜索的多样性，并在开发和探索之间实现了更好的平衡。

邻域评估过程在算法2中进行了说明。从随机选择的顶点𝑘 ∈ 𝑈(𝑋)（第4行）开始，VWDT𝑞尝试打开每个覆盖顶点𝑘的候选中心𝑖 ∈ 𝐶𝑘，即对所有𝑗 ∈ 𝑋更新相应的𝛿𝑗值，就好像候选中心𝑖已经被打开一样（第6–7行），以便能够快速计算出由此产生的邻近解的目标值𝑓(𝑋 ⊕ Swap(𝑖, 𝑗))。然后，我们遍历每个非禁忌移动，并记录最佳移动及其对应的交换操作（第9–16行）。当所有关于打开候选中心𝑖的尝试移动都被评估后，𝛿值恢复到邻域评估开始之前的值（第18行）。

此外，算法3中给出了子程序TryToOpenCenter()。根据目标函数（12），如果在打开中心𝑖之前，只有一个中心𝑙 ∈ 𝑋覆盖顶点𝑣，那么关闭中心𝑙的𝛿值将减少𝑤𝑣（第3–5行）。原因在于，一旦中心𝑖被打开，关闭中心𝑙将不再使顶点𝑣变为未覆盖状态，因此惩罚减少。我们仅关注关闭中心时的𝛿𝑗（∀𝑗 ∈ 𝑋），因为算法2中的第8–17行仅包含关闭另一个中心的操作。在最坏情况下，算法2和算法3的时间复杂度分别为𝑂(𝑛²)和𝑂(𝑛)。此外，当我们最终做出最佳移动（算法1，第7行）时，应以类似方式更新受影响的𝛿值。

4.5. 混合双禁忌策略

禁忌搜索是一种强大的基于局部搜索的元启发式算法，用于解决各种组合优化问题（Glover, 1989）。它通常基于基于最近访问的禁忌列表来禁止重新访问最近探索过的解。

理想情况下，所有评估过的解都不应再次访问。然而，如果我们以这种方式系统地探索解空间，所提出的VWDT𝑞将不再是启发式算法，并且必须面对精确算法的缺点和局限性。相比之下，传统的基于属性的禁忌搜索方法通常记录最近访问解的有限特征，并有助于搜索跳出局部最优陷阱。它简单高效，但可能会误判解的禁忌状态。因此，有前景的邻域移动可能会被错误地禁止，所以必须仔细调整诸如禁忌期限等合成参数。在设计VWDT𝑞算法时，我们试图结合它们的优点，并在完整性和收敛速度之间取得平衡。因此，它结合了基于属性和基于解的禁忌策略（Wang et al., 2017），这可以导致不同的搜索轨迹，并有助于搜索跳出局部最优陷阱。对于基于解的禁忌策略，我们不禁止所有评估过的解，而仅禁止实际访问过的解。

让我们回顾一下，在模型（𝑆𝐶𝑞𝑤）的解向量中，每个项𝑥𝑗表示顶点𝑗是否被选择为中心。基于属性的禁忌策略防止立即关闭新打开的中心。具体来说，在基于属性的禁忌策略中，禁忌期限𝑡𝑡的参数固定为两次迭代。特别是，如果我们在当前迭代𝑖𝑡𝑒𝑟中设置𝑥𝑗 = 1，则在下一个𝑡𝑡迭代中禁止将𝑥𝑗重置为0。换句话说，直到迭代𝑖𝑡𝑒𝑟 + 𝑡𝑡，基于属性的禁忌列表𝐴𝐿中都将有一个条目{𝑗}。

基于解的禁忌策略背后的思想与数学规划中的行生成方法类似。当解𝑋被记录为禁忌状态时，可以将其视为向模型（𝑀𝐶𝐿𝑤𝑞）添加了一个惰性约束\sum_{j\in X}x_{j}\leq p-1。如果最终执行了交换移动，获得了新的当前解𝑋，则将𝑋的禁忌状态保存到基于解的禁忌列表𝑆𝐿中，并永久禁止再次访问它。在技术上，我们以高效但不准确的方式实现了基于解的禁忌列表。VWDT𝑞使用哈希函数ℎ将解向量𝑋映射到整数值ℎ(𝑋) ∈ [0, 𝐿)（𝐿 = 10⁸），并且基于解的禁忌列表𝑆𝐿是一个二进制向量，其中SL(h(X))=1当且仅当解𝑋已被访问。在出现哈希冲突导致一些未访问解的禁忌状态被错误识别的情况下，我们使用多个哈希函数ℎ𝑡（𝑡 = 1, 2, 3）来降低冲突率，即解𝑋处于禁忌状态当且仅当\bigwedge_{\mathrm{r}=1}^{3}SL^{I}(h^{t}(X))=1。我们将哈希函数ℎ^𝑡^定义为等式（13），其中𝛾_𝑡是一个常数参数，且𝛾1, 𝛾2, 𝛾3的值分别为1.3、1.9、2.3。

在VWDT中，同时使用了基于解和基于属性的禁忌策略。当交换移动满足这两个禁忌策略中的任何一个条件时，VWDT算法将不会接受它作为候选移动。

5. 实验结果与比较

为了证明VWDT的有效性，我们在三组共174个标准基准实例和一组336个大规模实例上进行了广泛的计算实验，并将VWDT与文献中最先进的算法进行了比较。

5.1. 实验方案

我们的VWDT算法使用C++编写，并通过Visual Studio 2017进行编译。所有计算实验均在具有Intel Xeon E5-2609v2 2.50 GHz CPU和32 GB RAM的Windows Server 2012 × 64系统上单线程执行。我们重新实现了PBS算法（Pullan, 2008），在5毫秒（20秒）的时间限制下，为顶点数少于（多于）70,000的每个实例获得覆盖半径𝑟𝑞0的良好初始上界。对于VWDT，它包括计算𝑟𝑞0的总时间以及从(𝑀𝐶𝐿𝑞0)到(𝑀𝐶𝐿𝑞∗)顺序解决所有子问题的总时间，其中𝑞∗是最佳覆盖半径𝑟𝑞∗的边长排名。除非另有说明，否则每个实例的结果是通过独立运行VWDT 20次获得的，并且每个决策子问题对应每个覆盖半径的时间限制为900秒。我们的实验中有四组实例。

1. ORLIB：第一组包含来自OR-Library1（Beasley, 1990）的40个𝑝-中位问题实例（pmed）。它们基于随机无向图，其中顶点数𝑛和中心数𝑝满足𝑛∈[100, 900]和𝑝∈[5, 90]，规模相对较小。
2. TSPLIB：第二组包含来自TSPLIB2（Reinelt, 1991）的98个TSP实例。这些实例基于平面图，通常来源于实际应用。其中有44个小规模实例（sTSP），顶点数范围从226到657，其余54个（u1060, rl1323, u1817, 和 pcb3038）被归类为大规模实例。中心数𝑝分布在5到500之间。
3. World TSP：第三组包含来自World TSP3（Reinelt, 1991）的36个TSP实例。这些实例基于六个国家的地图，分别表示为阿曼（mu1979）、加拿大（ca4663）、坦桑尼亚（tz6117）、瑞典（sw24978）、缅甸（bm33708）和中国（ch71009）。顶点数𝑛的范围从1979到71,009，这在它们的名称中已明确给出，中心数𝑝的范围从5到100。
4. Massive TSP：最后一组基于TSPLIB4（Reinelt, 1991）中的大规模图。该完整数据集首先由Contardo等人（2019）使用，然后由Gaar和Sinnl（2022）研究。这组大规模TSP实例之前仅用于测试精确算法。顶点数𝑛的范围在1621到238,025之间，这在它们的名称中已明确给出，中心数𝑝的范围从2到30。根据中心数的不同，该组进一步分为9个数据集，分别是P2、P3、P5、P10、P15、P20、P25和P30。

对于所有实例，距离矩阵𝒅并未直接给出，因此我们使用Floyd算法（Floyd, 1962）为ORLIB实例计算所有顶点对之间的最短路径，并为TSPLIB、World TSP和Massive TSP实例计算欧几里得距离，以获得每对顶点𝑖和𝑗之间的距离𝑑𝑖𝑗。对于TSPLIB和World TSP，欧几里得距离四舍五入到最接近的百分位。对于Massive TSP，我们按照最近的文献中的做法，将距离四舍五入到最接近的整数，以便进行公平比较。

5.2. 参考算法

我们提出的VWDT算法在解的质量和达到最优解的计算时间方面，与五种精确算法（ELP、DBR2、CIK、SAT-sol和fCLH）、三种近似算法（Gon+、CDSh和CDSh+）以及六种元启发式算法（VNS、PBS、GRASP/PR、GRASP+PS、TSA和GMA）进行了比较。请注意，对于三种近似算法，我们仅报告了它们中的最佳结果。同时，我们还将VWDT算法与我们的初步VWTS算法（Zhang等人，2020）进行了比较。表1展示了参考算法的实验环境。列“Score”是从www.passmark.com获得的每篇文献中使用的处理器的单线程评分。为了尽可能公平地比较CPU时间，本节中所有算法的CPU时间都通过乘以Score/1356（分母为我们的CPU的单线程评分）进行了归一化处理，但VNS（Mladenović等人，2003）和DBR2（Calik和Tansel，2013）除外。由于VNS和DBR2的测试环境不明确，它们的CPU时间没有进行归一化处理。然而，由于VNS和DBR2获得的解的质量相对较低，这并不影响总体结论。

5.3. 参数设置

VWDT的参数设置如表2所示，这可以视为算法的默认设置，并贯穿本研究中的所有实验。我们的算法参数在列“Range”所示范围内，通过IRACE包（López-Ibáñez等人，2016）进行了测试和调优。IRACE包是一个自动算法配置工具，它实现了基于迭代竞赛的配置程序。所有参数的最终值记录在“Value”列中。此外，还引入了参数𝛾1、𝛾2和𝛾3来构建不同的哈希函数。请注意，𝛾𝑡的值对算法的性能不敏感。我们只需确保它们不要太大以避免溢出。

5.4. 计算结果

本节对VWDT的性能进行了全面研究。

5.4.1. 三个知名数据集

表3展示了VWDT在三个知名数据集上的总体结果。列“Set”和“Dataset”分别给出了基准实例集和数据集的名称。列“Count”展示了数据集中实例的数量。列“CPU”报告了我们的VWDT算法在每个数据集上的平均总CPU执行时间（以秒为单位）。列“CPU-𝑞∗”给出了VWDT解决对应于已知最佳覆盖半径𝑟𝑞∗的子问题所需的运行时间（以秒为单位），这表明当可以使用并行计算时，VWDT的性能可以显著提高。我们可以观察到，除了三个最大的数据集sw24978、bm33708和ch71009外，VWDT在20次独立运行中能够以100%的成功率获得最优解。一般来说，当顶点数少于10,000时，VWDT非常稳定，因为它在所有20次独立运行中都达到了这样的结果。

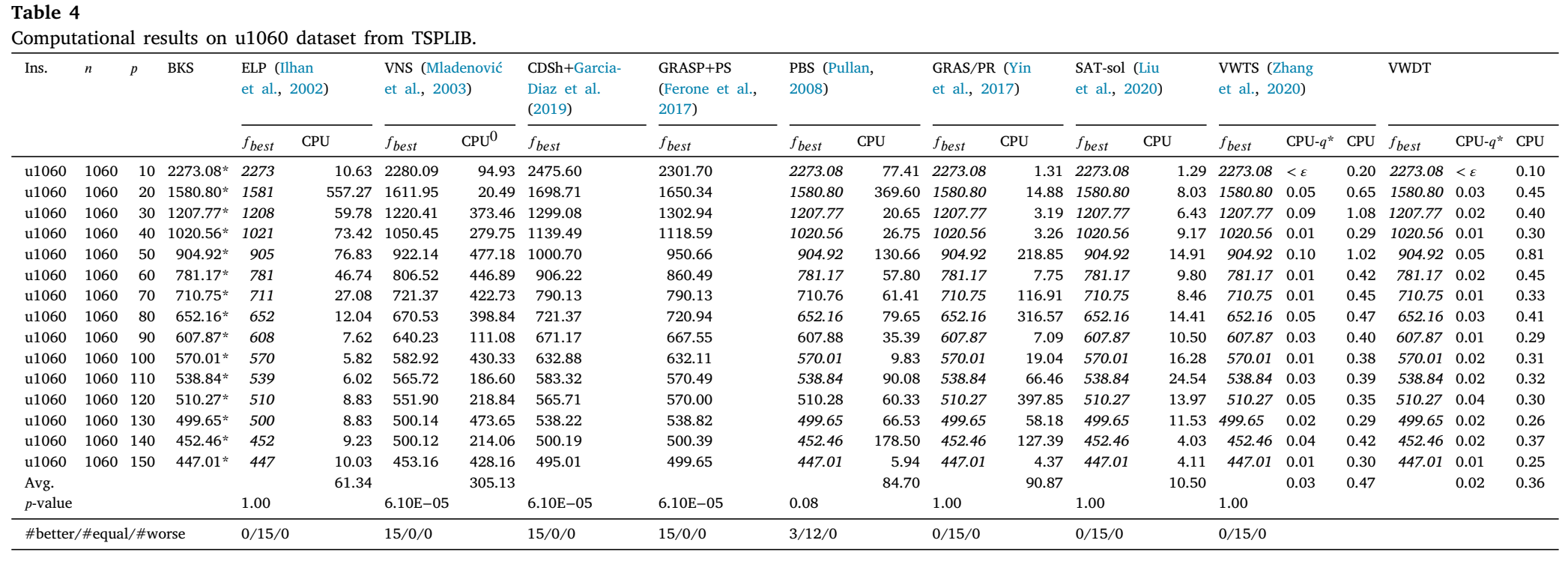
表格4至9报告了详细结果。由于大多数参考算法和提出的VWDT算法都能在1秒内获得pmed和sTSP数据集上所有实例的最优解，因此我们省略了这两个数据集的详细结果。5 这些表格遵循下文描述的相同约定。列“Ins.”给出了实例的名称。列“𝑛”和“𝑝”分别表示顶点和中心的数量。列“BKS”代表所有算法的最佳已知解的目标值。对于可以证明其最优目标值的实例，即模型（𝑀𝐶𝐿𝑞∗−1）的下界大于零，用“*”标记。具体来说，MIP模型在100小时的时间限制下使用Gurobi 8.1进行求解。列“𝑓𝑏𝑒𝑠𝑡”和“𝑓𝑎𝑣𝑔”分别给出了相应算法获得的最佳和平均目标值。显然，根据模型（𝑃 𝐶），𝑓𝑏𝑒𝑠𝑡越小越好。列“Hit”显示了在给定时间限制内达到最佳已知结果𝑓𝑏𝑒𝑠𝑡的成功率。列“CPU”报告了这些算法归一化后的平均总CPU执行时间（以秒为单位）（见第5.2节）。如果由于测试环境不明确，相应算法的CPU总执行时间未进行归一化处理，则用“CPU0”表示。对于VWDT算法，CPU时间包括使用PBS计算𝑟𝑞0以及顺序求解从（𝑀𝐶𝐿𝑞0）到（𝑀𝐶𝐿𝑞∗）的所有子问题的总时间，其中𝑞∗是最佳覆盖半径𝑟𝑞∗的边长等级。列“CPU-𝑞∗”给出了VWDT解决对应于最佳已知覆盖半径𝑟𝑞∗的子问题所需的运行时间（以秒为单位），这表明在可以使用并行计算时，VWDT具有很大潜力。#better、#equal和#worse分别表示VWDT与相应算法相比获得更好、相等和更差结果的实例数量。请注意，精确算法在找到最优解并证明其最优性之前不会停止，因此，对于小型实例，我们可能会省略它们对应的𝑓𝑏𝑒𝑠𝑡值。我们将小于0.01秒的计算时间记录为“< 𝜀”。如果某个算法未在特定实例上报告结果，则相应项将用短横线“-”标记。行“Avg.”显示了每个算法在相应数据集的所有实例上的平均计算时间。行“𝑝-value”用于验证VWDT与参考算法之间比较的统计显著性，该值来自对VWDT和参考算法的最佳值应用非参数Wilcoxon检验的结果。𝑝-值小于0.05表示存在统计学上的显著差异。此外，改进的最佳已知结果以粗体显示，而匹配的最佳结果则以斜体显示。

表格4至6将我们的VWDT的实验结果与ELP（Elloumi等人，2004）、DBR2（Calik和Tansel，2013）、VNS（Mladenović等人，2003）、PBS（Pullan，2008）、GRASP/PR（Yin等人，2017）、GRASP+PS（Ferone等人，2017）、Gon+、CDSh、CDSh+（Garcia-Diaz等人，2019）、SAT-sol（Liu等人，2020）和VWTS（Zhang等人，2020）在TSPLIB中的u1060、rl1323和u1817数据集上获得的结果进行了比较。

如表格4、5和6所示，提出的VWDT在𝑝=100时改进了GRASP/PR和PBS在rl1323上获得的先前最佳已知结果。除了改进解的质量外，VWDT在计算时间方面在u1060、rl1323和u1817实例上均优于其他所有算法。具体来说，VWDT在所有40个实例上均在5秒内获得了最优解，而PBS、GRASP/PR和SAT-sol在几个困难实例上可能需要超过1000秒才能收敛到其最佳解。此外，所提算法在一半实例中在0.5秒内达到了最佳结果，而PBS、GRASP/PR和SAT-sol在大多数实例上需要100到5000秒。对于u1060、r1323和u1817数据集，VWDT非常稳定，因为在所有20次独立运行中均达到了这样的结果。

数据集pmed、sTSP、u1060、rl1323和u1817已关闭，且VWDT能够在短时间内获得所有实例的最优解。图1展示了VWDT在已关闭实例上的整体优势，图中我们仅选择了几个表现最佳的算法进行比较，包括GRASP/PB、PBS、SAT-sol和VWTS。在这三张图表中，每个条形的高度代表计算时间不超过对应𝑥值所指定时间的实例数量。可以看出，VWDT在ORLIB实例和小型TSPLIB实例上的计算时间不超过0.05秒。然而，GRASP/PR、PBS和SAT-sol在几个难解的小型实例上可能需要数百秒才能收敛。

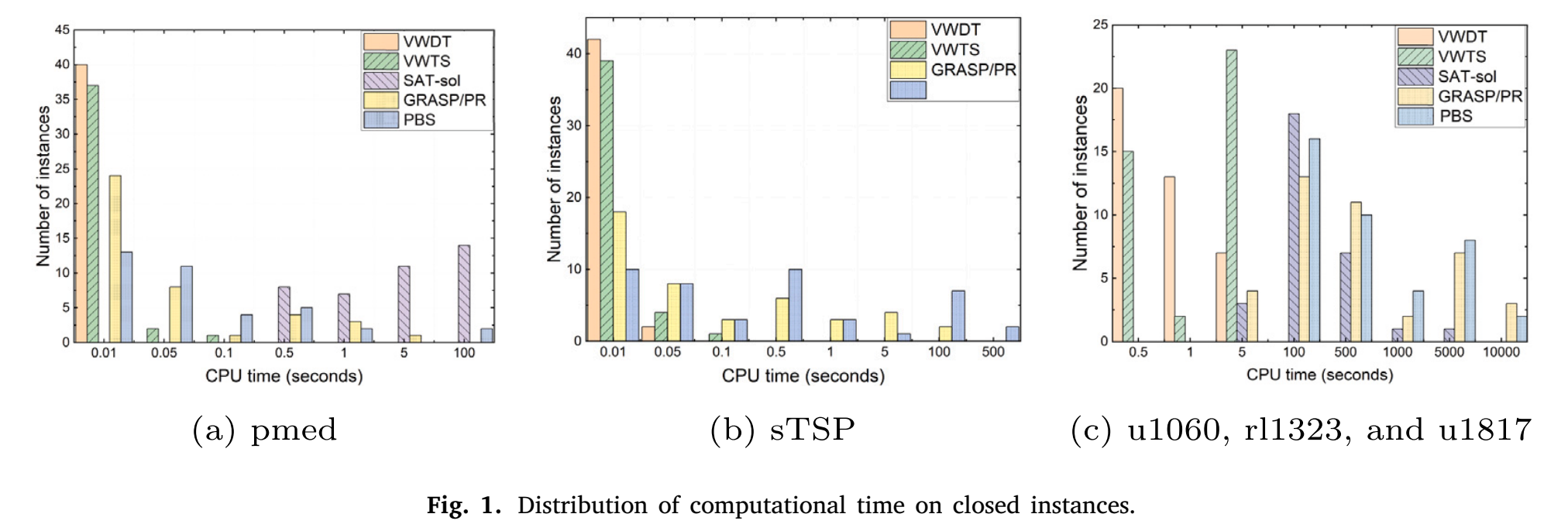
表7报告了针对TSPLIB中最具挑战性的数据集pcb3038的计算结果。VNS和GRASP+PS仅处理了𝑝 ≥ 50的实例。Gon+/CDSh和GRASP+PS没有报告它们的计算时间。从表7中我们可以观察到，VWTS和VWDT在𝑝 = 50, 100, 150, 200, 250, 300, 350, 400, 450, 500的10个实例上显著改进了已知的最佳结果。此外，VWDT在𝑝 = 50, 100, 150, 200的四个实例上进一步优化了VWTS获得的最佳结果。在改进的结果中，𝑝 = 450, 500的结果已被证明是最优的。就解的质量而言，我们的VWDT算法在所有pcb3038实例上均优于Gon+/CDSh、VNS和GPASP+PS算法。此外，从表3我们还可以观察到，获得新纪录的成功率仍为100%。除了新的上界外，VWDT的总计算时间比PBS和GRASP/PR短得多。与VWTS相比，我们的VWDT不仅提高了解决方案的质量，而且在总计算时间上几乎是VWTS的两倍快。较小的𝑝值（<0.05）表明，我们的最佳结果与所有参考算法（VWTS除外）的结果之间存在显著差异。

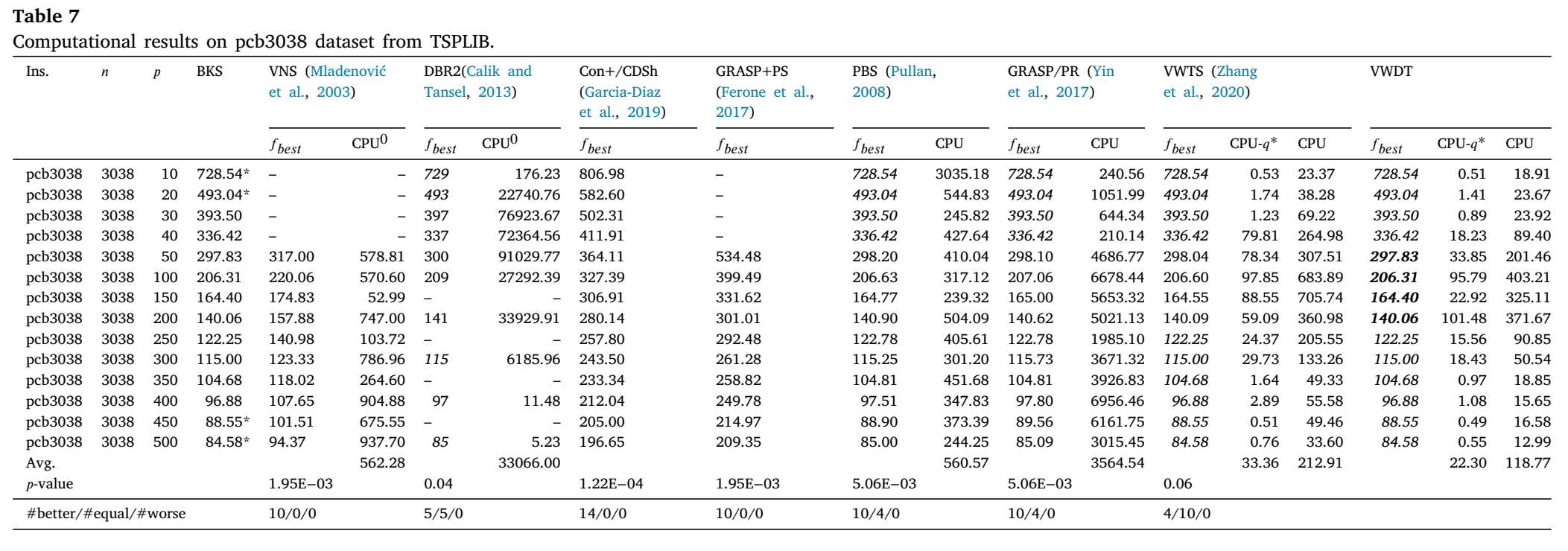
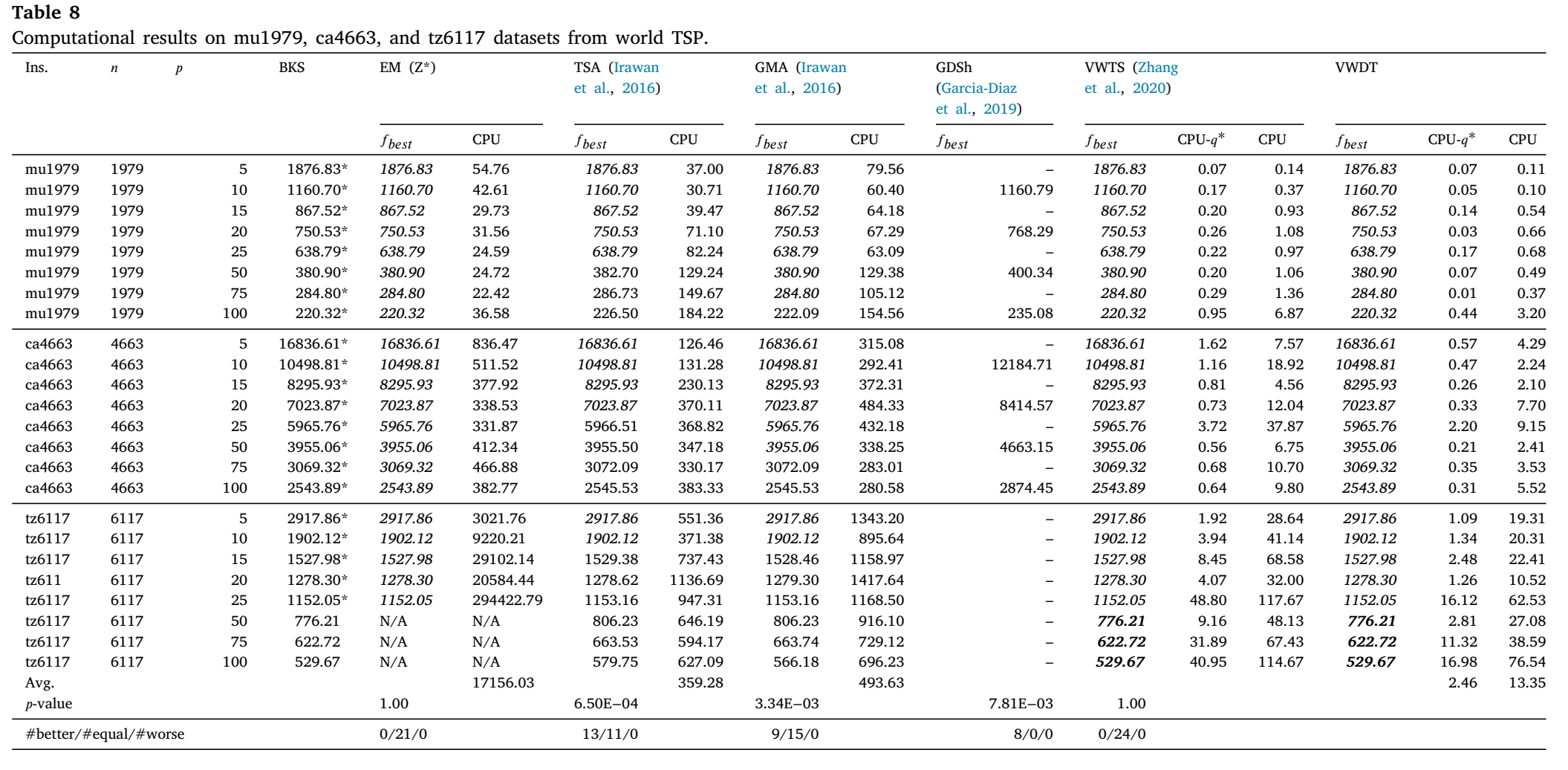
表8和表9报告了EM(Z*)、TSA、GMA（Irawan等人，2016年）、GDSh、Gon+（Garcia-Diaz等人，2019年）、VWTS（Zhang等人，2020年）以及我们提出的VWDT在World TSP的36个实例上的计算结果。从表8和表9中我们可以观察到，对于15个最优性未知的开放实例（tz6117在𝑝 = 50, 75, 100时，以及sw24978、bm33708和ch71009），在VWTS已经为4个实例（tz6117在𝑝 = 50, 75, 100时，以及sw24978在𝑝 = 25时）改进了最佳结果的基础上，VWDT为剩余的11个实例（sw24978在𝑝 = 50, 75, 100时，以及bm33708和ch71009）改进了最佳结果，并为其余实例匹配了最优解。对于表9，较小的𝑝值（<0.05）表明，我们的最佳结果与所有参考算法的结果之间存在显著差异。值得注意的是，VWDT在顶点数少于10,000的实例（mu1979、ca4663、tz6117）上保持了100%的成功率。总体而言，VWDT在解的质量和计算效率方面均优于TSA、GMA、Gon+和VWTS算法。

5.4.2. 大规模TSP集合

表10展示了由CIK（Contardo等人，2019年）、fCLH（Gaar和Sinnl，2022年）以及我们的VWDT在大规模集合上获得的整体结果。列“Count”显示了每个数据集中的实例数量。列“#best”表示相应算法在所有算法中获得最佳已知结果的实例数量。可以观察到，VWDT在所有实例上都获得了最佳已知结果，而没有任何参考算法能够取得如此全面的成果。与fCLH相比，我们的VWDT获得了138个更好的解，198个相等的解，且没有更差的解。与表现最佳的算法CIK相比，VWDT获得了65个更好的解，272个相等的解，且没有更差的解。当中心数量较少（𝑝 ≤ 5）时，我们的VWDT获得最佳已知结果所需的时间略长于CIK和fCLH。然而，随着中心数量的增加（𝑝 > 5），VWDT在解的质量和计算效率方面相对于CIK和fCLH的优势变得明显。表11展示了65个改进实例的详细信息。TL1和TL2分别是CIK和fCLH的运行时间限制，分别为24小时和1800秒。列“LB”给出了文献中精确算法获得的每个实例的下界。具体来说，对于实例tz6117 𝑝 = 25，VWDT获得的上界等于下界，即VWDT解决了这个实例。

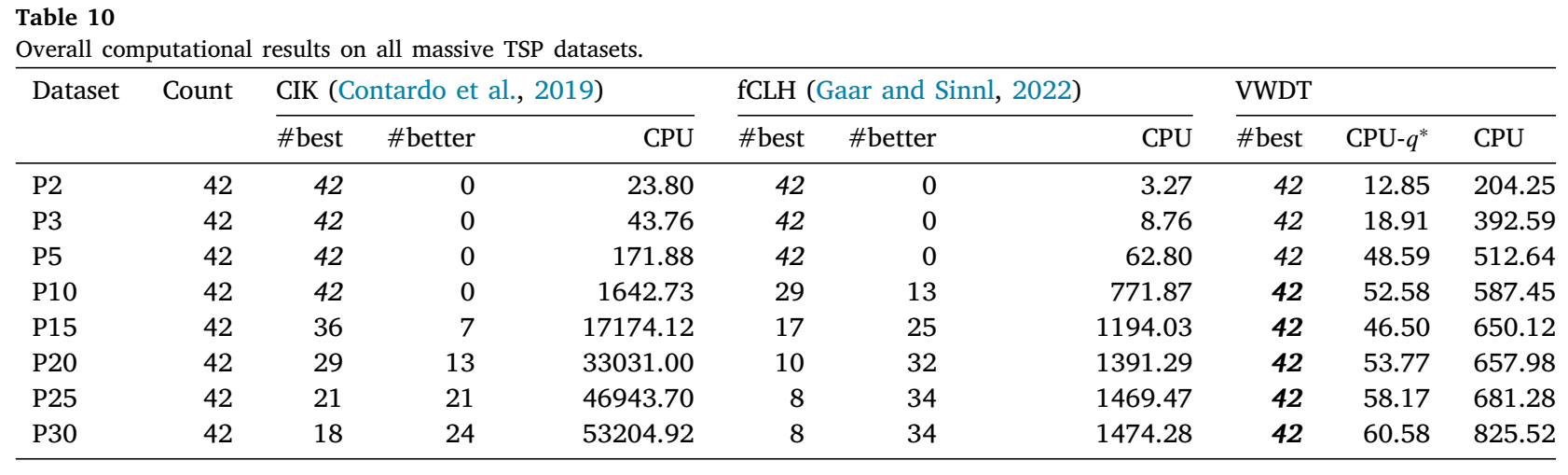
综上所述，这些统计数据表明，我们的VWDT在解决大规模𝑝-中心问题实例方面高度有效且高效。特别是当中心数量较大时，其在获得高质量上界方面的性能远优于精确算法。

6. 分析与讨论

6.1. 混合双禁忌策略的重要性

在我们的VWDT算法中，混合双禁忌策略在稳定产生高质量结果方面发挥着重要作用。为了验证混合双禁忌策略的有效性，我们针对TSPLIB中的大型难解数据集pcb3038进行了实验，将VWDT的原版与三个简化版——VW、VWDT-S和VWDT-A进行了比较。这四个版本除了禁忌策略的配置外，其他组件都相同。VW采用不带任何禁忌策略的局部搜索。VWDT-S仅采用基于解的禁忌策略，而VWDT-A仅启用基于属性的禁忌策略。对于每种算法，我们在pcb3038数据集上独立运行了20次。对于每个实例，每个对应于不同覆盖半径的子问题的时间限制为900秒。

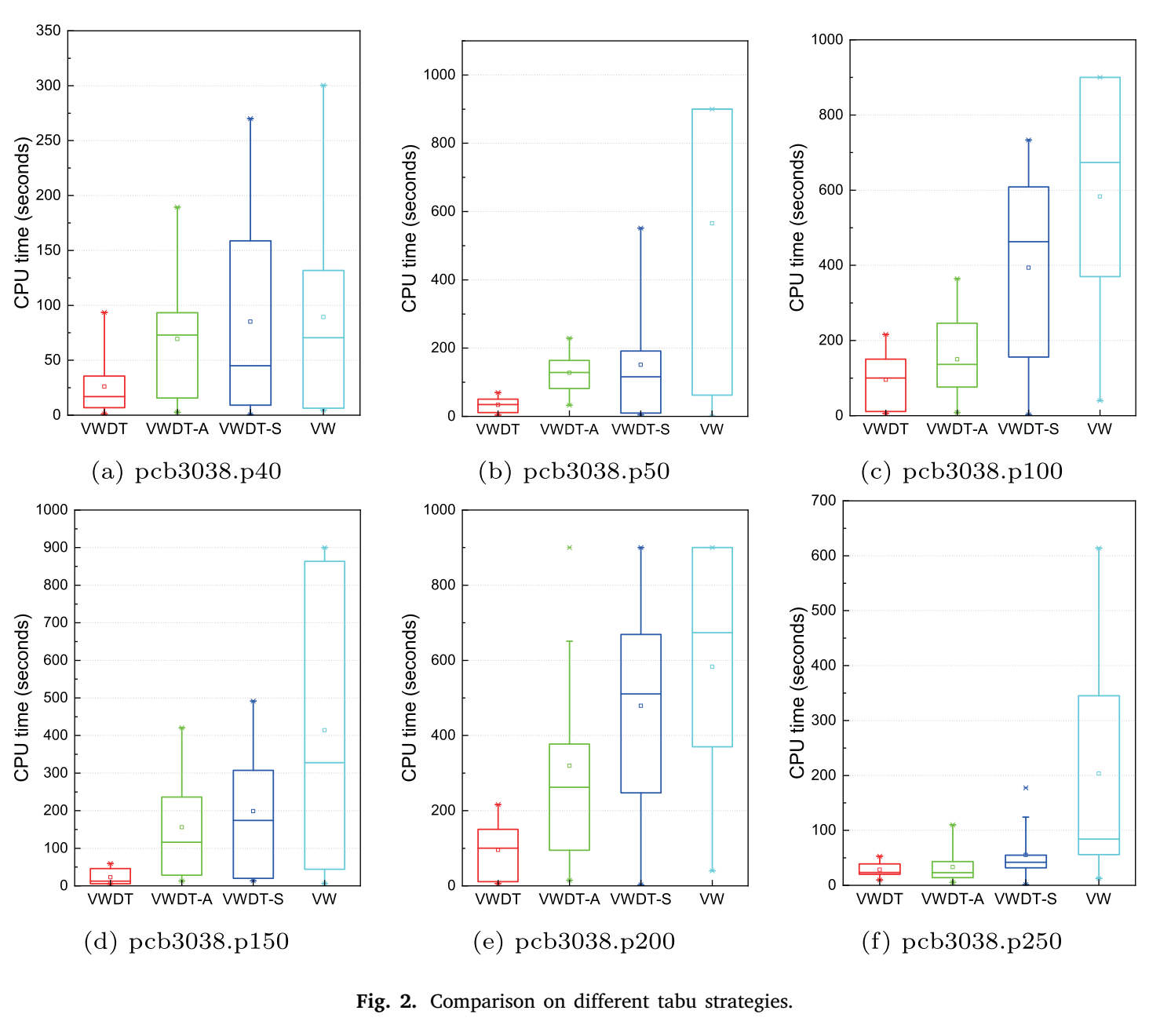
表12报告了VWDT、VW、VWDT-S和VWDT-A在pcb3038数据集上的实验结果。列𝑇𝑏𝑒𝑠𝑡和𝑇𝑎𝑣𝑔分别表示达到最佳已知结果𝑓𝑏𝑒𝑠𝑡所需的最佳和平均CPU时间。列Hit表示在给定的时间限制内达到最佳已知结果𝑓𝑏𝑒𝑠𝑡的成功率。此外，图2以箱形图的形式展示了VWDT、VW、VWDT-A和VWDT-S在六个代表性实例（𝑝分别为40、50、100、150、200、250的pcb3038）上消耗的计算时间的分布。

表12和图2表明，混合双禁忌策略优于其他三种策略。具体来说，表12显示，VWDT-A和VWDT-S在两个实例（𝑝分别为100、200的pcb3038）上未能始终匹配最佳已知解，而VW在四个实例（𝑝分别为50、100、150、200的pcb3038）上未能做到这一点。此外，对于𝑝为100和200的实例，VWDT-A和VWDT-S的命中率不是100%，而VW的命中率甚至低于50%。因此，VWDT比VW、VWDT-A和VWDT-S更稳定，因为其具有更高的命中率和更好的与最佳发现解的平均偏差。如图2所示，在计算效率方面，混合双禁忌策略在所有六个实例上明显优于其他变体。

6.2. 顶点加权技术的有效性

随着禁忌搜索的进行，越来越多的解被记录在基于解的禁忌列表中，这可能会将可行解空间缩小到不连续的区域，并可能阻碍基于轨迹的元启发式搜索。相比之下，顶点加权技术通过改变目标函数来帮助搜索跳出局部最优解，在提出的VWDT算法中发挥着重要作用。

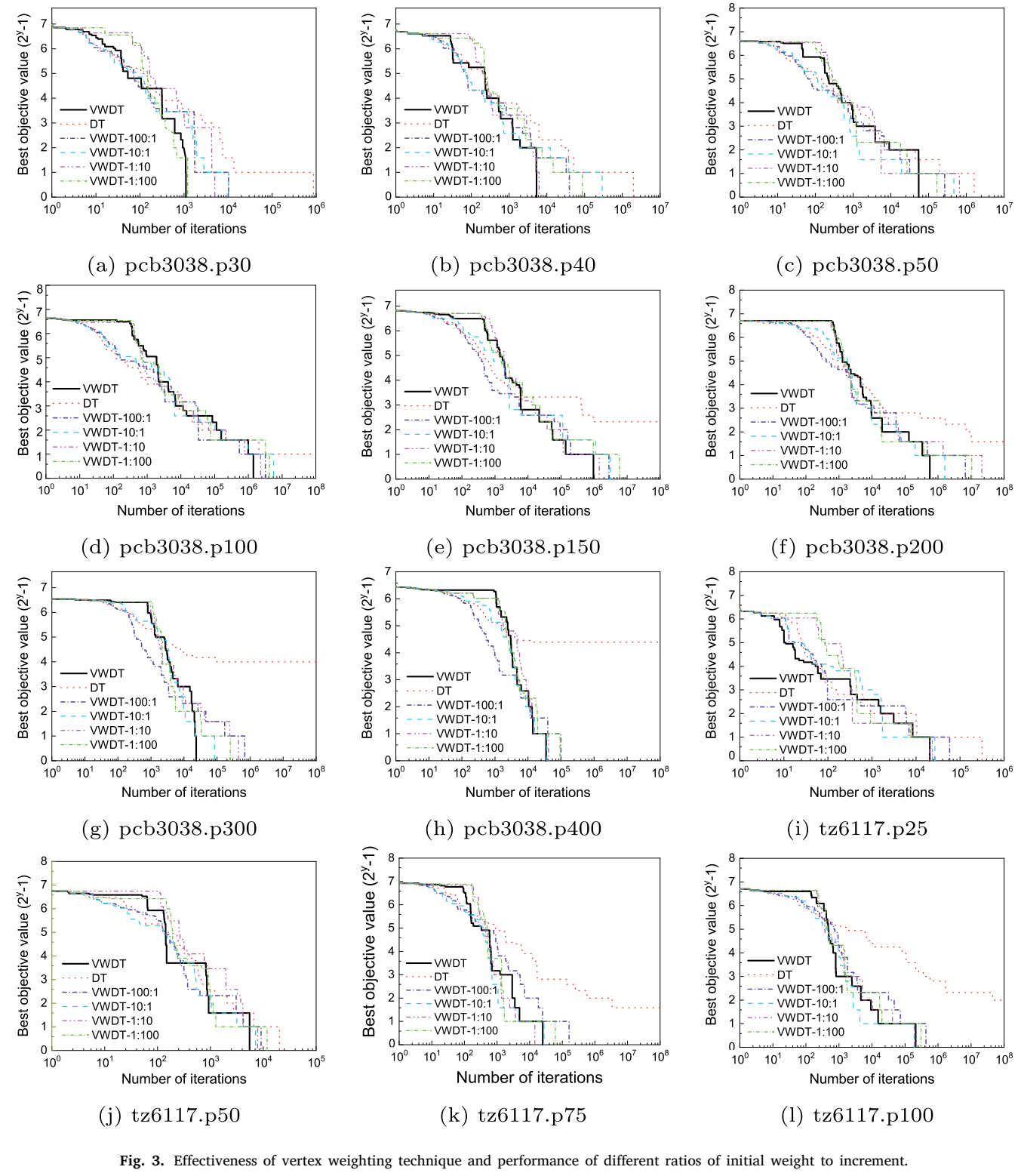
为了证明顶点加权技术的重要性，我们对12个难解实例进行了实验，以比较VWDT与其简化版的性能。具体来说，我们禁用了顶点加权技术以获得一个新的DT算法，然后将其与原始VWDT在大型实例上进行比较，这些实例包括𝑝值分别为30、40、50、100、150、200、300、400的pcb3038数据集，以及𝑝值分别为25、50、75、100的tz6117数据集。DT与VWDT的工作原理几乎相同，但DT在整个搜索过程中顶点权重始终为1，即算法1中的第11-13行被禁用。

此外，我们还分析了不同的顶点权重更新方案如何影响VWDT算法的有效性。初始权重与增量的比值控制着搜索的激进程度。如果增量太大，未覆盖顶点的惩罚将迅速增加，使得这些顶点在后续搜索中迅速被覆盖。如果增量太小，则可能需要很长时间才能重塑解空间格局并跳出局部最优解的盆地。为了找到增量的最佳值，我们测试了五个比值，分别是100:1、10:1、1:1、1:10和1:100。注意，在提出的VWDT算法版本中，如算法1所述，权重比例是1:1。为了公平比较，我们在每次运行时使用相同的随机种子，以便它们在每个实例上从相同的初始解开始。图3展示了随着搜索的进行，VWDT的变体（比值为100:1、10:1、1:1、1:10、1:100以及DT）中未覆盖顶点数量的演变。每个点(𝑥, 𝑦)表示在10𝑥次迭代后，有2𝑦 − 1个顶点没有被任何中心覆盖。我们可以观察到，在初始阶段，DT可以获得比VWDT更好的不可行解。然而，如前所述，禁忌搜索只是简单地禁止一个候选中心成为中心，而不是直接防止一个顶点不被覆盖。可以想象，在极端情况下，搜索可能根本不会考虑覆盖一些难以覆盖的客户。不出所料，在所有12个实例上，经过104次迭代后，VWDT的表现都优于DT。图3显示，VWDT的所有五个变体在所有12个实例上都优于DT，并且随着𝑝的增大，差距也在扩大。根据图3，在初始阶段，初始权重与增量的比值越高，算法收敛得越快。然而，在搜索的后期阶段，它们的收敛速度逐渐降低。在12个实例中，有10个实例在收敛速度方面，权重比例为1:1的VWDT获得了比其他权重比例更好的整体结果，而在剩下的2个实例（图3(k)和3(l)）中，其表现略差或与一两个算法相当，这凸显了顶点加权策略的有效性。这些观察结果证实，顶点加权对于VWDT获得竞争性结果至关重要。

7. 结论

本文研究了𝑝-中心问题，并设计了一种元启发式算法——基于顶点加权的双禁忌搜索（VWDT），以解决这一经典且具有挑战性的NP难问题。我们将𝑝-中心问题分解为一系列决策子问题，并通过结合混合双禁忌搜索与顶点加权技术来解决每一个子问题。在文献中广泛使用的510个基准实例中，VWDT改进了其中84个实例的最佳已知结果，而对于其余所有实例，则达到了文献中的最佳记录。实验结果表明，VWDT在解的质量和计算效率方面都具有高度竞争力。此外，我们还进行了实验，以分析VWDT中的关键要素，如顶点加权技术和双禁忌策略。实验显示，这两个组成部分在搜索的探索和利用之间达到了良好的平衡，从而使VWDT既强大又稳健。

成功解决𝑝-中心问题激发了我们未来的研究兴趣，即探索将基于解和基于属性的禁忌策略与加权技术相结合。由于这些策略独立于𝑝-中心问题，因此将它们应用于其他优化问题似乎很有前景。