具有新的邻域结构的作业车间调度问题禁忌搜索算法
编辑摘要
禁忌搜索(TS)算法是解决作业车间调度问题(JSP)的最有效方法之一,而JSP是最难解决的NP完全问题之一。然而,对于JSP的禁忌搜索而言,邻域结构和移动评估策略在其有效性和效率方面起着核心作用。本文提出了一种新的增强型邻域结构,并将其应用于通过禁忌搜索方法解决作业车间调度问题。使用这种新的邻域结构,结合适当的移动评估策略和参数,我们在一组标准基准实例上测试了禁忌搜索方法,并在未解决的实例中发现了大量更好的上界。计算结果表明,对于矩形问题,我们的方法在解决方案质量和性能方面都优于其他所有方法。
- 关键词:作业车间调度问题;完工时间;启发式方法;禁忌搜索
1. 引言
作业车间调度问题旨在最小化调度的完工时间,即J\|C_{\mathrm{max}},该问题具有非常广泛的工程背景。该问题可简要描述如下:存在一组作业和一组机器。每个作业由一系列操作组成,每个操作使用其中一台机器固定时长。每台机器一次最多处理一个操作。一旦操作开始,则不允许抢占。调度是将操作分配给机器上的时间段。该问题的目标是找到一个调度,使其最小化完工时间(C_{\mathrm{max}}),即最后一个操作完成的时间。
JSP是最难的组合优化问题之一。由于它是一个重要的实际问题,JSP已被大量研究人员研究,并提出了许多优化算法和近似算法。优化算法主要基于分支定界(B&B)方案,如Carlier和Pinson [1]以及Brucker等人 [2]的研究,已成功应用于解决小型实例。然而,它们无法在合理时间内解决大于250个操作的实例。另一方面,近似算法,包括优先调度、移位瓶颈法、元启发式方法等,为JSP提供了很好的替代方案。近似算法最初是基于调度规则开发的,这些规则非常快,但它们提供的解决方案的质量通常有很大的提升空间。一个更精细的算法是Adams等人 [3]提出的移位瓶颈法,该算法能以更高的计算成本产生更好的近似解。最近,元启发式方法,如遗传算法(GA)[4]、模拟退火(SA)[5]、禁忌搜索(TS)[6,7],能够在合理的计算时间内提供高质量的解决方案,并引起了众多研究人员的关注。相关综述可见Vaessens等人 [8]、Blazewicz等人 [9]以及Jain和Meeran [10]的研究。
在元启发式方法中,由Glover [11]最初提出的禁忌搜索似乎是解决以完工时间为标准的作业车间调度问题(JSP)最有前途的方法之一。Taillard [12]首先将禁忌搜索应用于JSP,其主要贡献是使用了Van Laarhoven等人[5]引入的邻域结构,并提出了一种快速估计策略。Taillard观察到,该算法在处理矩形实例时具有更高的效率。自此以后,研究人员对Taillard的原始算法进行了许多改进,其中最重要的贡献包括Nowicki和Smutnicki [7]、Dell'Amico和Trubian [13]、Barnes和Chambers [14]以及Chambers和Barnes [15]。在这些单独的禁忌搜索方法中,Nowicki和Smutnicki [7]设计的TSAB算法在效率和有效性方面为JSP带来了真正的突破。例如,它仅在一台现已过时的个人电脑上用了30秒就找到了臭名昭著的实例FT10的最优解。Nowicki和Smutnicki的i-TSAB技术[16]是他们早期TSAB算法的扩展,代表了JSP当前最先进的近似算法,并改进了大多数未解决实例的上界。
随着JSP禁忌搜索算法的改进,为了提高搜索的有效性和效率,已经提出了不同的邻域结构和评估策略。在本文中,通过深入研究以往的邻域策略,我们提出了一种新的增强型邻域结构,以解决通过禁忌搜索方法解决的作业车间调度问题。我们的方法在一组标准基准实例上进行了测试,并为未解决的实例找到了54个更好的上界。本文的其余部分组织如下。第2节给出了作业车间调度问题的表示。第3节提供了新的邻域结构和禁忌搜索方法的实现。第4节首先分别比较了不同的邻域结构和移动评估策略,然后给出了基准问题的计算研究。第5节是结论。
2. JSP的表示
作业车间调度问题可以通过Balas [17]引入的析取图来表示。设J=\{1,2,\ldots,n\}为作业集合,M=\{1,2,\ldots,m\}为机器集合。析取图G:=(V,A,E)定义如下:V是\{0,1,2,\ldots,\tilde{n}\}的节点集合,代表所有操作,其中0和\tilde{n}分别表示虚拟的开始和结束操作。A是连接同一作业连续操作的联结(有向)弧的集合,而E是连接由同一机器k处理的操作的析取弧的集合。更确切地说,E=\bigcup_{k=1}^{m}E_{k},其中E_{k}是与机器k对应的析取对弧的子集;E中的每个析取弧都可以看作是一对方向相反的弧。弧(i,j)\in A的长度为P_i,表示处理时间。每个\operatorname{arc}(i,j)\in E的长度根据其方向为p_{i}或p_{j}。以表1中给出的三个作业和三个机器为例。该问题可以用图1所示的析取图来表示。
根据Adams等人[3]的方法,通过移除析取弧,图G可以分解为直接子图D=(V,A),以及通过删除联结弧和虚拟节点0和\tilde{n}从G获得的m个团G_{k}=(V_{k},E_{k})。在E_{k}中的选择S_{k}包含E_k中每对方向相反的弧之间的一个有向弧。如果不包含任何有向环,则选择是无环的。此外,对机器k进行排序意味着在E_k中选择一个无环选择。完整选择S由每个E_{k}中的一个选择S_{k}的并集组成,其中k\in M。完整选择S,即将析取弧集E替换为联结弧集S,会产生有向图D_{s}=(V, A\cup S);如果有向图D_{s}是无环的,则完整选择S也是无环的。无环选择S定义了一个调度,即问题的一个可行解。图2表示了图1中析取图的一个可行解。此外,如果L(u,v)表示在D_{s}中从u到v的最长路径的长度,则调度的完工时间L(0,\tilde{n})等于D_{s}中最长路径的长度。因此,在析取图的语言中,解决作业车间调度问题就是找到一个无环完整选择S\subset E,以最小化有向图D_{s}中最长(关键)路径的长度。
表1:三个任务和三台机器的一个例子
| Job | (Machine sequence, Processing time) | ||
|---|---|---|---|
| j1 | (1,3) | (2,2) | (3,5) |
| j2 | (1,3) | (3,5) | (2,1) |
| j3 | (2,2) | (1,5) | (3,3) |
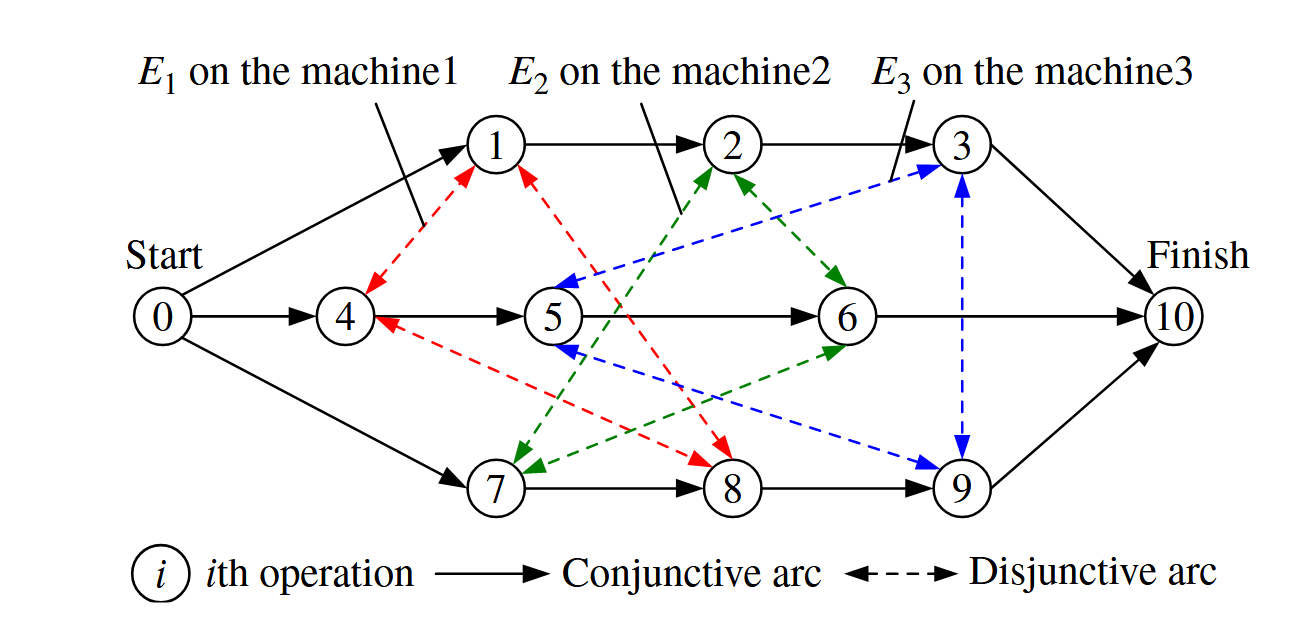
图1. 一个具有 n=3、m=3 和 \tilde{n}=10 的实例的析取图

图2. 图1中析取图的一个可行解。
一个可行解的关键组成部分是关键路径,它是有向图 D_{s}=(V,A\cup S) 中从起点到终点的最长路线,其长度代表工期 C_{\mathrm{max}}。关键路径上的任何操作都被称为关键操作。在图2中,关键路径的长度为19,关键路径为{0,4, 1, 8, 9, 3, 10}。还可以将关键路径分解为若干个区块。区块是指在同一台机器上处理的最大相邻关键操作序列。在图2中,关键路径被分为两个区块,B_{\mathrm{1}}=\{4,1,8\} 和 B_{2}=\{9,3\}。任何操作 u 都有两个直接的前驱和后继,即作业前驱和后继,分别用 JP[u] 和 JS[u] 表示,以及机器前驱和后继,分别用 MP[u] 和 MS[u] 表示。换句话说,(JP[u],u) 和 (u,JS[u]) 是联结图 D_{s} 的弧,(MP[u],u) 和 (u,MS[u])(如果存在的话)是 S 的弧。任何局部搜索算法(如禁忌搜索)的核心都是邻域,简而言之,邻域是通过对给定可行解进行微小扰动而获得的一组可行解。在作业车间调度问题(JSP)中,微小扰动通常是通过重新排列关键路径上的操作顺序来产生的,并且只有通过这种重新排列,才可能产生工期优于当前解的邻域解。
3. 作业车间调度问题的禁忌搜索算法
禁忌搜索算法,主要由Glover[1820]定义和发展,已成功应用于大量组合优化问题,特别是在生产调度领域。禁忌搜索是对著名的爬山启发式算法的改进,它使用记忆功能来避免陷入局部最小值。

图3. 禁忌搜索算法的通用流程图
禁忌搜索(TS)过程通常很简单。该过程从一个可行的初始解开始,并将其存储为当前种子和最优解。然后,通过邻域结构生成当前种子的邻域解。这些邻域解是候选解。它们通过目标函数进行评估,并选择其中最优且未被禁忌或满足期望准则的候选解作为新的种子解。这个选择被称为移动,并被添加到禁忌表中;如果禁忌表超载,则移除另一个(最旧的)移动。如果新的种子解优于当前最优解,则将其存储为新的最优解。迭代过程重复进行,直到满足停止准则。图3展示了禁忌搜索算法的流程。在本节的其余部分,将详细介绍我们增强的动态禁忌搜索(TS_{ED})算法。
3.2. 新的邻域结构
邻域结构是一种机制,通过对给定解应用微小扰动来获得一组新的邻域解。每个邻域解都可以通过从一个给定解进行一步移动而直接到达[20]。邻域结构直接影响禁忌搜索(TS)算法的效率。因此,如果可能的话,必须消除不必要的和不可行的移动。作业车间调度问题(JSP)的第一个成功的邻域结构是由Van Laarhoven等人[5]提出的,通常表示为N1^1^[9]。N1邻域是通过交换同一台机器上任意相邻的一对关键操作而生成的,并基于以下性质:
- 给定一个可行解,交换两个相邻的关键操作不会得到一个不可行解。
- 非关键操作的排列不能改善目标函数,甚至可能产生一个不可行解。
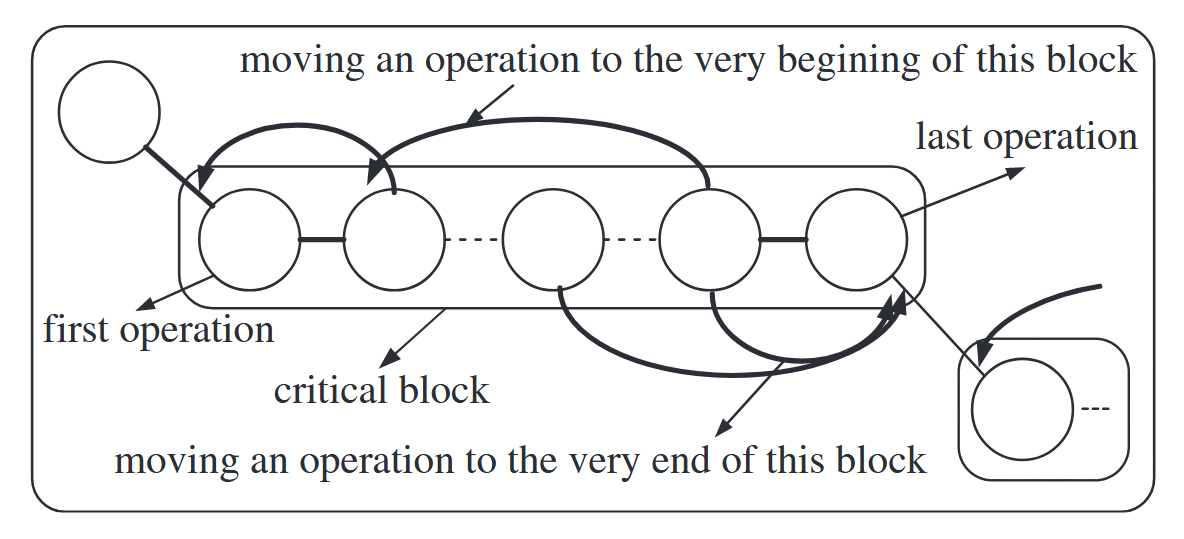
图4. N4移动的邻域。

图5. N5移动的邻域。
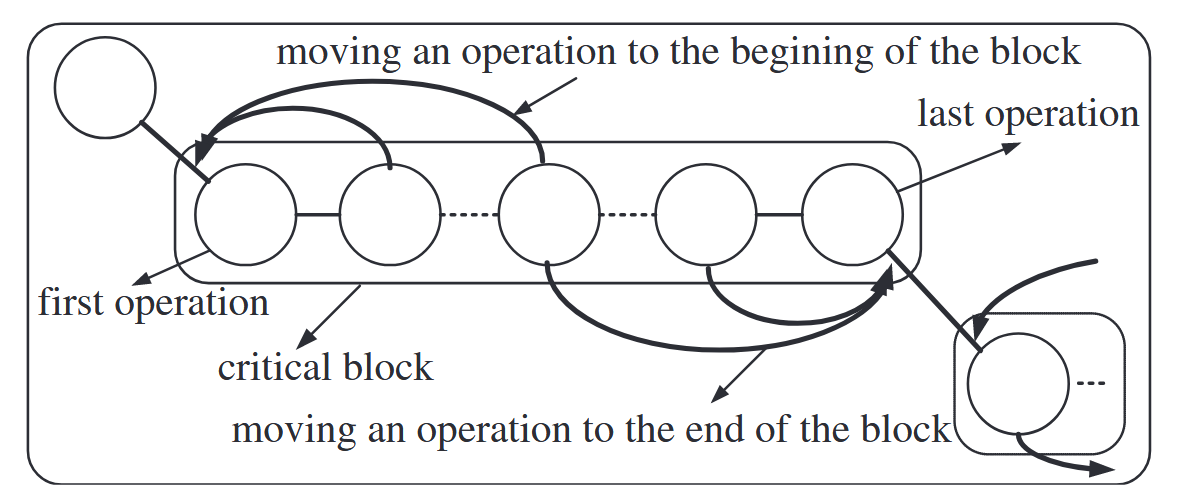
图6. N6移动的邻域。
然而,N1邻域的大小相当大,包含了大量未改进的移动。Matsuo等人[21]的一个重要观察结果是,除非u的前置作业或\upsilon的后置作业在关键路径P(0,n)上,否则包含u和v的交换不能减少工期,即在一个块内交换内部操作永远不会立即改善工期。因此,Dell'Amico和Trubian(N4)^2[13])、Nowicki和Smutnicki(N5)[7]以及Balas和Vazacopoulos(N6)[22]提出了进一步精细化的邻域。N4、N5和N6邻域分别如图4-图6所示。这些最近广为人知的邻域主要基于块的概念,其中一个移动是通过将一个操作插入到关键块的前端或后端来定义的。N5邻域涉及单个边界弧的反转,并且比其他邻域小得多,而N4和N6邻域则同时涉及多个不相交弧的反转,因此可以探索一个相当大的邻域。N6邻域也被视为N5邻域的扩展,它比N4邻域受到更多的限制,但目前是最有效和高效的邻域结构之一(见第4.1节的表2)。

图7. 进一步扩展的邻域结构。
根据Matsuo等人[21]的研究,为了通过交换u和v(假设u在v之前处理)来实现改进,JP[u]或JS[v]必须位于关键路径P(0,n)上,即u或v必须是关键块的第一个或最后一个操作。因此,我们提出了一种进一步扩展的邻域结构,其中移动被定义为将一个操作插入到块的开始或结束位置,或者将关键块的第一个或最后一个操作移动到块内的内部操作位置(如图7所示)。这导致了一个相当大的邻域,并探索了一个更广泛的空间。然而,需要探索的问题是:在哪些条件下,对关键操作u和v的交换可以保证不会产生循环,以及如何减小邻域的大小。接下来,我们为我们的邻域结构给出两个定理及其证明。考虑一个可行解s:
定理1。如果两个在同一台机器上执行的操作u和v都位于关键路径P(0,n)上,且L(v,n)\geqslant L(JS[u],n),则将u移动到v之后会得到一个无环的完全选择。
证明。采用反证法:假设将u移动到v之后会产生一个循环C。那么C包含(u,JS[u])或(u,MS[v])。如果(u,JS[u])\in{C},则在D_{s}中存在从JS[u]到v的路径(循环是JS[u]→v→u→JS[u]),因此L(JS[u],n)>L(v,n),这与假设相矛盾。如果(u,MS[v])\in{C},则在D_{s}中存在从MS[v]到v的路径,这与D_{s}是无环的假设相矛盾。这完成了证明。
定理1得出了以下结论:如果在D_{s}中不存在从JS[u]到v的有向路径,那么将关键操作u移动到关键操作v之后不会产生循环。
类似地,我们得到了定理2。
定理2。如果两个在同一台机器上执行的操作u和v都位于关键路径P(0,n)上,且L(0,u)+p_{u}\geqslant L(0,JP[v])+p_{JP[v]},则将v移动到u之前会得到一个无环的完全选择。
证明。与定理1的证明类似。
为了构建我们的邻域结构,我们实际上扩展了Balas和Vazacopoulos提出的命题2.2和2.3的范围,并提出了定理1和定理2。定理1和定理2可以应用于在同一台机器上执行的任意两个关键操作u和v的交换,无论关键路径上是否包含JS[u]或JP[v]。在实验中,我们观察到由定理1和定理2构建的邻域比类似的N4邻域更简单且受到更多的约束。因此,我们的搜索邻域可以通过在可行解S上对两个关键操作u和v进行如下交换来获得:
(1)如果包含u和v的关键路径P(0,n)也包含JS[v],则将u插入到v之后;
(2)如果包含u和v的关键路径P(0,n)也包含JS[v],则将v移动到第一个连续内部操作之前;
(3)如果包含u和v的关键路径P(0,n)也包含JP[u],则将v插入到u之前;
(4)如果包含u和v的关键路径P(0,n)也包含JP[u],则将u移动到第一个连续内部操作之后(见图5)。
假设对两个操作u和v的交换导致新调度相对于旧调度的工期增加。那么显然,新调度中的每条关键路径都包含弧(v,u)[22]。我们可以利用这一事实进一步减小邻域的大小。
3.3. 移动评估
作业车间调度问题(JSP)中禁忌搜索(TS)算法的运行时间通常主要取决于每次移动的计算成本。因此,为了提高算法效率,已经提出了多种邻域评估策略,如精确方法和估计方法。Ten Eikelder等人[23]提出的称为bowtie的过程是JSP中最有效的精确方法,它仅重新计算移动后需要更新的操作的头部和尾部值。然而,即使这种精确方法对于较大规模的实例仍然需要非常长的计算时间。为了加速搜索过程,已经提出了可以快速筛选出那些有很大可能性将搜索导向新精英解的移动的估计方法。Taillard[6]提出了一种快速估计方法。Nowicki和Smutnicki[16]则提出了该策略的一种更精确的方法,并应用于著名的i-TSAB算法中。但这些估计策略仅适用于交换关键块的相邻操作。Balas和Vazacopoulos[22]提出的一种重要估计策略可以一次反转多个析取(即非互斥的)操作,并且Balas和Vazacopoulos的过程也是解决JSP最高效的实现之一。
在本文中,我们使用自己的算法(见第4.2节)比较了Ten Eikelder等人的精确方法与Balas和Vazacopoulos的估计方法。第4.2节的实证测试表明,与精确方法相比,估计方法减少了20%到40%的计算量,并且随着实例规模的增大,搜索效率也在提高。直觉上,人们可能认为精确方法在解的质量上会比估计方法更好,但实证结果表明,与精确方法相比,估计方法也能实现更低的平均相对误差(MRE),从而否定了这一直觉。
3.4. 禁忌表和移动禁忌状态
禁忌表的目的是防止搜索过程回到之前步骤中已经访问过的解。禁忌表中存储的元素是移动的属性,而非解的属性。使用这种属性的主要目的是节省计算机内存。在我们的邻域结构中,每一步选择的移动可能会反转一个或多个析取弧,并涉及一系列操作。在本文中,与之前的禁忌搜索(TS)算法不同,我们不仅在禁忌表中记录操作的序列,还记录它们在机器上的位置。这种方法能更好地表示移动的属性。更准确地说,如果移动包含u和v的交换,那么在该移动被标记为“禁忌”期间,不允许实现相同操作序列和位置(即从u到v的操作(u,\ldots,w,\ldots,v)以及从u到v在机器上的位置(p_u,\ldots,p_w,\ldots,p_v))的移动。此外,必须指出,禁忌状态的定义是基于移动的属性。实施“部分属性”禁忌表的一个副作用是,它可能会给未访问的解,甚至是有趣的解,赋予禁忌状态。避免这个问题的一种方法是使用渴望准则,即只要移动的总完成时间低于迄今为止找到的最佳解的总完成时间,就接受该移动。
禁忌表的长度决定了元素在内存中保留的时间限制,这在当前迭代中是不被鼓励的。因此,它对搜索过程有影响。如果列表长度太短,则无法避免循环;相反,如果长度太长,则会产生太多限制。根据我们的实验研究,适当“短”的禁忌表长度便于在已访问区域进行深入的搜索,并可能找到更好的解,而较长的禁忌表长度则适用于搜索的多样化,引导搜索探索更大的区域。然而,在作业车间调度问题(JSP)中如何有效设置禁忌表的长度仍然是一个未解决的问题,并且设置参数通常需要进行繁琐的试错。一项实证研究表明,如果允许在搜索过程中动态改变禁忌表的长度,则可能找到高质量的解。例如,Taillard[6]建议从给定最小值和最大值之间的范围内随机选择禁忌表的长度,并在每次迭代一定数量的次数后更改它。另一个例子是Dell'Amico和Trubian[13]提出的更为复杂的方法。
我们的初步实验表明,禁忌表的长度强烈依赖于作业和机器的数量,并且随着作业数量(n)与机器数量(m)之比的增大,合适的禁忌表长度也会增加。为了获得良好的结果,可以将禁忌表的最小长度设置为L=10+n/m。为了更有效地避免循环,我们应用了动态禁忌表,并在两个极值L_{\mathrm{min}}和L_{\mathrm{max}}之间随机选择禁忌表的长度。在大量实验中,我们发现这两个极值之间的范围不会太大,并且随着作业数量与机器数量之比的增大而增大。对于所考虑的问题,L_{\mathrm{min}}=[L]和L_{\mathrm{max}}=[1.4-1.5L]是合适的值。如果n\leqslant2m,则最大极值L_{\mathrm{max}}=[1.4L];否则,L_{\mathrm{max}}=[1.5L]。然而,在我们的实验中,每迭代一定数量的次数就改变禁忌表大小的方法并不总是显示出明显的优越性。因此,在我们的方法中,禁忌表的长度只是简单地在给定的最小值和最大值之间随机选择。
3.5. 移动选择
禁忌搜索(TS)方法的选择规则是选择非禁忌且具有最低完成时间(makespan)的移动,或者满足期望标准的移动。然而,可能会出现所有可能的移动都是禁忌的,且没有一个能满足期望标准的情况。在这种情况下,我们的程序会随机地从可能的移动中选择一个移动。
3.6. 终止准则
当迭代次数或不改进的移动次数达到最大值,或者证明解是最优时,算法停止。如果满足以下条件之一,则算法停止:(1) 所有关键操作都在同一台机器上处理(即只生成一个关键块)或属于同一作业(即每个块只包含一个操作),(2) 完成时间等于已知的下界,那么解是最优的,算法终止。
4. 计算实验
上述增强的动态禁忌搜索(TS_{ED})算法在奔腾IV 1.8G个人计算机上用VC++语言实现,并对大量来自文献的标准实例进行了测试。这些作业车间调度实例包括以下类别^4^:Fisher和Thompson [24]提出的三个实例(FT6、FT10、FT20),Lawrence [25]提出的四十个实例(LA01至LA40),Adams等人[3]提出的五个实例(ABZ5至ABZ9),Storer等人[26]提出的二十个实例(SWV01至SWV20),Yamada和Nakano [27]提出的四个实例(YN1至YN4),以及Demirkol等人[28]提出的八十个实例(DMU01至DMU80)。对于这些基准测试集,最佳已知上界(UB_{best})和最佳已知下界(LB_{best})取自Jain和Meeran [10],并根据Nowicki和Smutnicki [16]的改进结果进行了更新。为了评估解的质量,我们根据最佳已知下界(LB_{best})和由我们算法求解的最佳解的上界(即完成时间,UB_{solve}),使用“相对偏差”公式RE=100\times(UB_{solve}-LB_{best})/LB_{best},计算每个问题实例的平均相对误差(MRE)。
TS_{ED}算法从使用随机化的Gifler和Thomson算法生成的随机活跃解开始,禁忌表长度的选择见第3.4节,迭代次数设置为5000万次。不改进移动的数量根据特定条件设置。例如,在比较邻域策略时,不改进移动的数量设置为3000次;在比较估计方法和精确方法时,设置为100万次。在本节的其余部分,前两节分别比较了邻域策略和移动评估策略,以分析本文使用的新邻域结构和估计策略,最后一节则对我们算法在大量基准测试实例上的性能进行了评估。
4.1. 邻域策略的比较
下文测试并比较了六种邻域结构。它们分别表示为NS1(van Laarhoven等人,1992年,N1)、NS2(Chambers和Barnes,1994年)、NS3(Nowicki和Smutnicki,1996年,N5)、NS4(对Dell′Amico和Trubian,1993年的N4进行修改)、NS5(Balas和Vazacopoulos,1998年,N6)。最后,NS6表示我们提出的新邻域结构。
表2 六种邻域结构的比较
| NS6 | NS5 | NS4 | NS3 | NS2 | NS1 | |
|---|---|---|---|---|---|---|
| MC_max | 1416 | 1420 | 1415 | 1462 | 1473 | 1600 |
| MRE | 3.31 | 3.51 | 3.45 | 5.52 | 5.84 | 12.6 |
| NBE | 32 | 33 | 32 | 26 | 24 | 20 |
| MEN | 106 163 | 70216 | 127140 | 48973 | 48510 | 107649 |
| MNI | 5731 | 5468 | 5619 | 6690 | 6206 | 4149 |
| CPU-time | 298 | 205 | 462 | 121 | 134 | 307 |
同时,NS1、NS2、NS3和NS5在文献中都是知名的邻域。除了N1外,这些邻域都是基于区块的概念。更多信息,请参见第3.2节和Blazewicz等人[9]的研究。NS4与Dell'Amico和Trubian提出的N4略有不同。NS4邻域根据Dell'Amico和Trubian的方法,将区块内的操作移动到该区块的开始或结束位置,但在关键路径包含u和v且既不包含JS[u]也不包含JP[v]的情况下,不允许u和v互换。
为了准确评估这些邻域结构,我们使用TS_{ED}算法作为平台,唯一不同的是邻域结构。初始解由最短处理时间(SPT)优先调度规则生成,禁忌表的长度设置为12(除NS1采用Taillard的方法外),这是根据Geyik和Cedimoglu[29]的建议。邻域中的每个移动都进行了精确评估。当不改进移动的数量达到3000时,算法终止。测试了包含72个实例的基准测试集FT、LA、ABZ、SwV和YN。此外,还提出了几个用于比较的统计指标。它们分别是平均完成时间C_{\max}(MC_{\max})、找到的等于已知最佳解的解的数量(NBE)、评估的邻域数量的平均值(MEN)、迭代的平均次数(MNI)以及所有实例中消耗的总CPU时间(CPU-time)。
表2总结了与六个邻域相关的计算结果。NS6在六个邻域结构中提供了最小的MRE值。NS4(优于原始N4)提供的MRE接近NS6,但NS4消耗的计算时间过多。NS5比NS3、NS2和NS1更有效,而NS3优于NS2和NS1。总的来说,可以看出NS6是JSP的一个有效邻域结构。
4.2. 估算方法与精确方法的比较
我们使用TS_{ED}算法作为测试平台,比较了Balas和Vazacopoulos提出的估算方法与Ten Eikelder等人建议的精确评估方法(见表3)。两个测试平台在除移动评估方法外的所有方面均相似。为了进行更详细的性能比较,我们从FT、LA和ABZ基准测试集中选择了15个最难的实例。其中大多数实例都被视为计算挑战,甚至ABZ8和ABZ9实例的最优解仍未知。在实验中,算法从随机生成的活跃解开始,当找到最优解或改进移动的数量达到100万时终止。在表3中,列“LB”列出了Jain和Meeran中给出的已知最佳下界,接下来的列“Best”、“Avg”、“Worst”和“T_{\mathrm{av}} (s)”分别表示算法在10次运行中获得的最佳完成时间、平均完成时间、最差完成时间和平均计算时间(以秒为单位),最后一列“T_{\mathrm{estima}}/T_{\mathrm{exact}}”表示估算方法的平均计算时间T_{\mathrm{av}}与精确方法的平均计算时间T_{\mathrm{av}}的比率。最后一行显示了最佳相对误差(b-MRE)、平均相对误差(avg-MRE)和T_{\mathrm{estima}}/T_{\mathrm{exact}}的平均值,这些可用于分析两种评估方法的性能。
表3显示,与Ten Eikelder等人[23]的精确评估方法相比,Balas和Vazacopoulos的估算方法在评估移动时快了24倍。在实验中,估算方法不仅更快地找到了解决方案,而且能够实现略低的最佳相对误差(b-MRE)和平均相对误差(avg-MRE),因此表现优于精确方法。此外,表3还表明,对于14个实例(其中4个实例表现更好),估算方法产生的最佳完成时间优于或等于精确方法产生的最佳完成时间,唯一例外是LA40(在这种情况下,精确方法给出的最佳完成时间达到了最优解1222)。对此的一个合理解释是,估算策略扩大了下一次迭代的选择范围,从而使搜索能够探索更大的解空间。因此,在以下部分中,我们实现了Balas和Vazacopoulos提出的估算方法来进行每个移动的这些计算。
表3 Balas的估算方法与Ten Eikelder的精确方法的比较

4.3. 计算研究
首先,我们仍然考虑上面选出的十五个最难的问题实例。为了进行更详细的性能分析,我们将我们的TS_{ED}算法与目前最好的近似算法进行了比较,并使用以下符号表示这些算法:TSSB代表Pezzella和Merelli[30]提出的受移动瓶颈启发的禁忌搜索方法,BV代表Balas和Vazacopoulos[22]提出的受移动瓶颈启发的引导式局部搜索,SB-RGLS5代表Balas和Vazacopoulos的SB-RGLS5过程的解,BV-best代表Balas和Vazacopoulos获得的最佳解,TSAB代表Nowicki和Smutnicki[7]提出的禁忌搜索。考虑到测试中使用的计算机速度差异较大,我们没有详细列出计算时间。表4显示了这些算法针对这十五个难题的完成时间性能统计。
由于TS_{ED}算法的随机性,我们将TS_{ED}算法的平均性能(avg-MRE)与其他算法的结果进行了比较。总体而言,在不考虑运行时间的情况下,TS_{ED}算法提供的解决方案质量优于TSSB和TSAB,且接近BV的质量。此外,对于如LA27和LA29这样的矩形问题,TS_{ED}算法在解决方案质量和计算时间方面均优于其他算法。例如,TS_{ED}算法能够在个人电脑上几秒钟内获得LA27的最优解1235,而SB-RGLS1在CI-CPU时间上用了788秒才找到最优解。值得注意的是,TS_{ED}算法为LA29-1156和ABZ7-657找到的解决方案优于其他算法。这些基准实例的结果表明,我们的TS_{ED}算法在处理矩形问题时可能更有效。
为了进一步分析TS_{ED}算法,我们测试了Storer等人[26]生成的一些更大规模的50\times10实例(SWV11, SWV12, SWV13, SWV14, SwV15)。表5给出了SWV11-15实例的详细结果。这些结果是算法运行三次后选择的。在表中,列出了问题名称、问题维度、最佳上界和下界、迭代次数、最佳完成时间、达到最佳完成时间所需的计算时间以及其他算法获得的解决方案。同时,iTSAB代表Nowicki和Smutnicki[16]提出的禁忌搜索算法,CSSAW代表Steinhofel等人[31]提出的模拟退火过程。值得注意的是,TS_{ED}算法在解决方案质量上明显优于其他三种算法。我们找到了3个最优解,并改进了其余2个实例的上界,这些上界明显优于之前已知的最佳值,且非常接近下界。此外,TS_{ED}算法在SwV11-15实例上的MRE为0.05%,而最近最好的算法之一iTSAB算法在5000万次迭代中仅达到MRE=0.51%。在个人电脑上,TS_{ED}算法在大约1分钟(即0.5百万次迭代)内达到了MRE=1.19%,而要达到类似的目标,BV算法在SUNSPARC-330上大约需要120-180分钟。CS_{\mathrm{SAW}}在没有时间限制(t\rightarrow\infty)的情况下达到了MRE=1.1%。因此,我们得出结论,当作业数大于机器数时,TS_{ED}算法在解决方案质量和计算时间方面都更有效和高效。
表4 十五个难题FT、LA和ABZ的计算结果

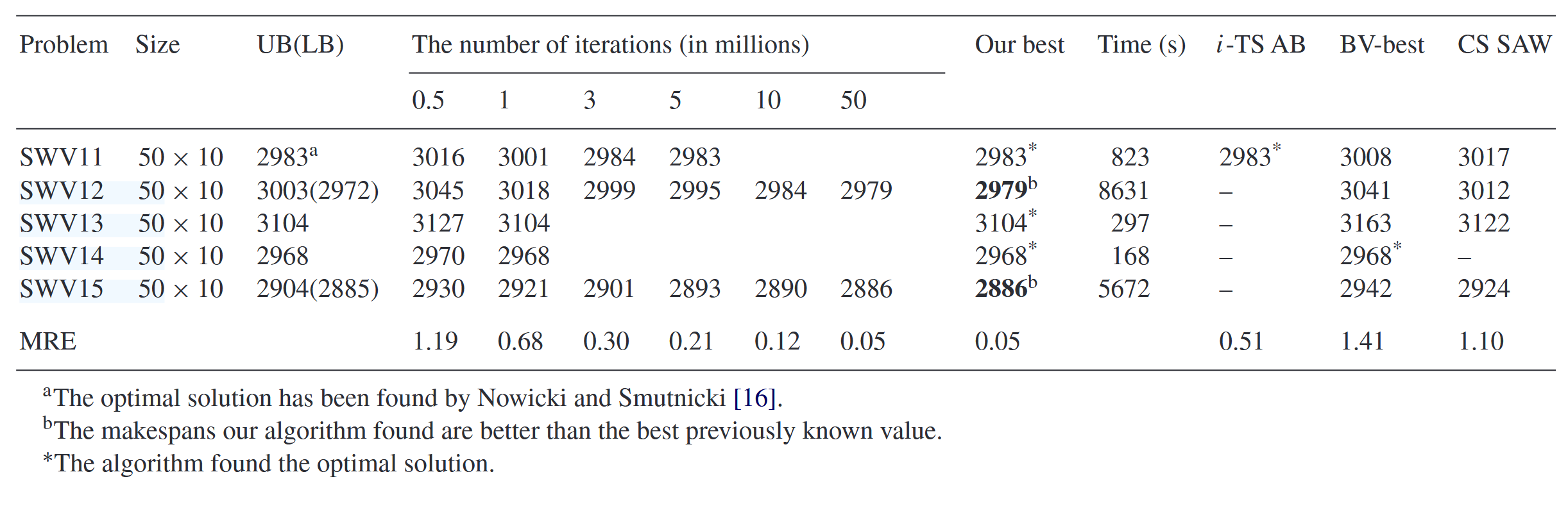
表5 Storer等人(1992)问题实例的结果
最后,我们在DUM基准测试集上测试了TS_{ED}算法。DMU类包含80个实例(操作数i的范围为300\leqslant i\leqslant1000),其中22个实例的最优解已知(主要位于DUM01-40实例中)。DMU41-80实例被认为特别难,因为它们满足2_{\mathrm{SETS}}原则,并且这些实例的最优解尚未得知。在本文中,我们改进了未解决的58个DUM实例中的51个的上界,详见表6。同时,对于DUM13和DUM26,所找到的结果提供了最优解,即:DUM13-3681和DUM26-4647。这些结果是在算法运行三次后得出的。表6列出了算法找到新上界的所有实例。
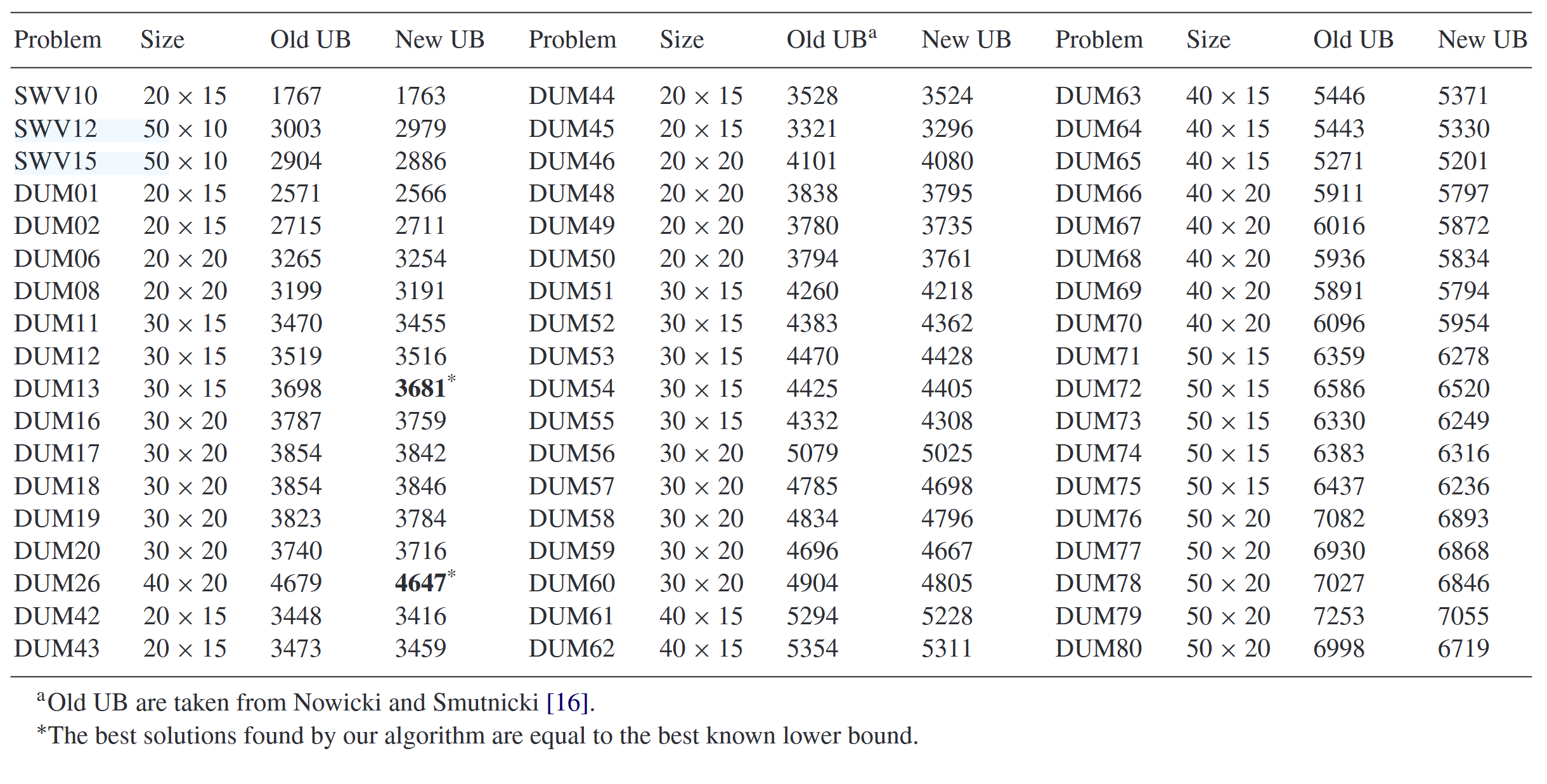
表6 算法找到的新上界
大多数DUM1-80实例之前的上界是由Nowicki和Smutnicki提出的著名i-TSAB算法[16]找到的。在本文中,我们的TS_{ED}算法改进了DUM实例中i-TSAB算法找到的大部分上界。此外,当n\geqslant2m时,TS_{ED}算法为所有未解决的DUM1-80实例找到了更好的工期(见表6)。因此,可以肯定的是,对于矩形实例,TS_{ED}算法在解的质量上优于i-TSAB算法。尽管测试所用的计算机速度不同,但对于矩形DUM实例,TS_{\mathrm{ED}}算法通常在5.1亿次迭代之前就能获得i-TSAB算法找到的上界(对于操作数300\leqslant i\leqslant600的实例,在500万次迭代之前;对于操作数600<i\leqslant1000的实例,在1000万次迭代之前),而i-TSAB算法则需要5000万次迭代才能达到上界。总体而言,对于矩形实例,我们的TS_{\mathrm{ED}}算法在解的质量和性能上都优于i-TSAB算法。
5. 结论
禁忌搜索(Tabu Search,TS)算法在解决作业车间调度问题(Job Shop Scheduling Problem,JSP)时的有效性和效率取决于其邻域结构和移动评估策略。然而,为了提高搜索效率,JSP中定义的邻域结构正变得越来越受限,如Nowicki和Smutnicki提出的极具限制性的邻域结构。因此,这种TS算法容易陷入局部最优解,而基于记忆最近访问情况的精英解恢复和循环检查机制被用来克服这一问题。在本文中,我们构建了一种新的邻域结构,它能够避免循环并探索更大的解空间。我们将这种新的邻域结构与其他五种邻域策略进行了比较,并证实它对于JSP是一种有效的邻域结构。此外,我们还研究了邻域评估策略的影响。实证测试表明,Balas和Vazacopoulos引入的估计方法不仅显著提高了搜索效率,而且对解的质量没有实质性影响。最后,我们在一组标准基准实例上测试了我们的方法,并改进了大量上界,这进一步验证了所提邻域结构的有效性。
本文为JSP提出的算法简单且易于实现。对于矩形问题(即作业数大于或等于机器数的JSP),该算法在解的质量和性能上甚至优于复杂的i-TSAB算法。例如,当n\geqslant2m时,我们的算法改进了i-TSAB算法为未解决的DUM1-80实例找到的所有上界。i-TSAB算法无疑是当前JSP领域的最先进的算法。然而,在本文中,我们怀疑当n\leqslant2m时,i-TSAB算法可能是解决JSP的一个非常强大的工具,但对于矩形问题,由于高度受限的邻域结构的限制,i-TSAB算法并不总是表现更好。此外,我们坚信,对于矩形问题,具有强大邻域结构和动态禁忌表的禁忌搜索可能比多起点TS方法更有效。这对于实际应用非常有用,因为在实际调度问题中,作业数通常远大于机器数。
在本文中,我们主要关注邻域结构的性能,并未提及禁忌搜索的多样化策略。因此,这可能是未来研究的一个课题。实现多样化的一个有前途的方法可能是应用多个邻域或长期记忆机制。此外,如何在JSP中有效设置禁忌表仍然是一个悬而未决的问题。越来越多的研究表明,短期记忆的长度会根据搜索条件的变化而动态变化,但仍有大量研究致力于寻找更好的实现方法。因此,未来的另一项研究可能是开发更有效的禁忌表策略。
- 1
- 0
-
分享
