110.平衡二叉树

要求：给定一个二叉树，判断它是否是平衡二叉树。

本题中，一棵高度平衡二叉树定义为：一个二叉树每个节点 的左右两个子树的高度差的绝对值不超过1。

需要区分两个概念：

• 二叉树节点的深度：指从根节点到该节点的最长简单路径边的条数。

• 二叉树节点的高度：指从该节点到叶子节点的最长简单路径边的条数。

自己在做题的时候遇见深度比较多。

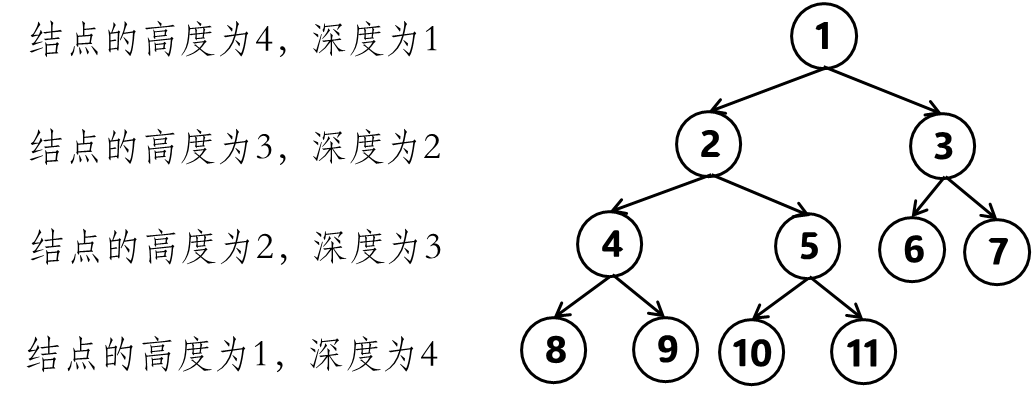
关于根节点的深度究竟是1 还是 0，不同的地方有不一样的标准，leetcode的题目中都是以节点为一度，即根节点深度是1。但维基百科上定义用边为一度，即根节点的深度是0，我们暂时以leetcode为准。

因为求深度可以从上到下去查 所以需要前序遍历（中左右），而高度只能从下到上去查，所以只能后序遍历（左右中）。

递归的思路

这道题需要判断是否为平衡二叉树，需要比较左右两个子树的高度，就需要后序遍历。

递归三部曲分析

1. 明确递归的参数和返回值

• 参数：当前传入的结点

• 返回值：以当前传入结点为根节点的树的深度

  • 如果当前传入节点为根节点的二叉树已经不是二叉平衡树了，还返回高度的话就没有意义了。

  • 此时可以返回 -1

2. 明确终止条件

• 递归的过程中依然是遇到空节点了为终止，返回0，表示当前节点为根节点的树高度为0

3. 明确单层递归的逻辑

• 分别求出左右子树的高度

• 如果差值小于1，返回当前高度

• 否则返回 -1，表示其已经不是平衡二叉树了

int leftHeight = getHeight(node->left); // 左
if (leftHeight == -1) return -1;
int rightHeight = getHeight(node->right); // 右
if (rightHeight == -1) return -1;

int result;
if (abs(leftHeight - rightHeight) > 1) {  // 中
    result = -1;
} else {
    result = 1 + max(leftHeight, rightHeight); // 以当前节点为根节点的树的最大高度
}

return result;

可以精简代码如下：

int getHeight(TreeNode* node) {
    if (node == NULL) {
        return 0;
    }
    int leftHeight = getHeight(node->left);
    if (leftHeight == -1) return -1;
    int rightHeight = getHeight(node->right);
    if (rightHeight == -1) return -1;
    return abs(leftHeight - rightHeight) > 1 ? -1 : 1 + max(leftHeight, rightHeight);
}

实现的代码

class Solution {
public:
    bool isBalanced(TreeNode* root) {
        int height = getHeight(root);
        return height != -1;
    }

    int getHeight(TreeNode* node) {
        if (node == nullptr)    return 0;
        int leftHight = getHeight(node -> left);
        int rightHight = getHeight(node -> right);
        if (leftHight == -1 || rightHight == -1)    return -1;
        if (abs(leftHight - rightHight) > 1)    return -1;
        else return max(leftHight, rightHight) + 1;
    }
};

257. 二叉树的所有路径

经典的回溯问题。

class Solution {
public:
    vector<int> path;
    vector<string> result;
    vector<string> binaryTreePaths(TreeNode* root) {
        path.push_back(root -> val);
        backTracing(root);
        return result;
    }

    void backTracing(TreeNode* root) {
        // 终止条件：当前是叶子结点
        if (!root -> left && !root -> right) {
            // 将path添加到result中
            string str;
            str += to_string(path[0]);
            for (int i = 1; i < path.size(); i++) {
                str += "->";
                str += to_string(path[i]);
            }
            result.push_back(str);
            return;
        }
        if (root -> left) {
            path.push_back(root -> left -> val);
            backTracing(root -> left);
            path.pop_back();
        }

        if (root -> right) {
            path.push_back(root -> right -> val);
            backTracing(root -> right);
            path.pop_back();
        }
    }
};

在写代码的时候，我有一点忘了考虑，就是在初始的时候向path添加根结点的值。如果只有根结点一个元素，代码会直接输出空的path路径，最终发生错误。

题解代码如下：

// 版本一
class Solution {
private:

    void traversal(TreeNode* cur, vector<int>& path, vector<string>& result) {
        path.push_back(cur->val); // 中，中为什么写在这里，因为最后一个节点也要加入到path中 
        // 这才到了叶子节点
        if (cur->left == NULL && cur->right == NULL) {
            string sPath;
            for (int i = 0; i < path.size() - 1; i++) {
                sPath += to_string(path[i]);
                sPath += "->";
            }
            sPath += to_string(path[path.size() - 1]);
            result.push_back(sPath);
            return;
        }
        if (cur->left) { // 左 
            traversal(cur->left, path, result);
            path.pop_back(); // 回溯
        }
        if (cur->right) { // 右
            traversal(cur->right, path, result);
            path.pop_back(); // 回溯
        }
    }

public:
    vector<string> binaryTreePaths(TreeNode* root) {
        vector<string> result;
        vector<int> path;
        if (root == NULL) return result;
        traversal(root, path, result);
        return result;
    }
};

精简的代码：

class Solution {
private:

    void traversal(TreeNode* cur, string path, vector<string>& result) {
        path += to_string(cur->val); // 中
        if (cur->left == NULL && cur->right == NULL) {
            result.push_back(path);
            return;
        }
        if (cur->left) traversal(cur->left, path + "->", result); // 左
        if (cur->right) traversal(cur->right, path + "->", result); // 右
    }

public:
    vector<string> binaryTreePaths(TreeNode* root) {
        vector<string> result;
        string path;
        if (root == NULL) return result;
        traversal(root, path, result);
        return result;

    }
};

自己写的和题解的主要区别是我自己写的代码在递归函数调用前就先push元素到path中，而题解是在调用后最开始的位置push元素。

404.左叶子之和

计算给定二叉树的所有左叶子之和。

也是经典的回溯问题。

class Solution {
public:
    int sumOfLeftLeaves(TreeNode* root) {
        int sum = 0;
        calculate(root, sum);
        return sum;
    }

    void calculate(TreeNode* root, int& sum) {
        TreeNode* leftNde = root -> left;
        if (leftNde && !leftNde->left && !leftNde->right) {
            sum += leftNde -> val;
        }
        if (root->left)   calculate(root->left, sum);
        if (root->right)    calculate(root->right, sum);
    }
};

下面是题解的代码：

class Solution {
public:
    int sumOfLeftLeaves(TreeNode* root) {
        if (root == NULL) return 0;
        if (root->left == NULL && root->right== NULL) return 0;

        int leftValue = sumOfLeftLeaves(root->left);    // 左
        if (root->left && !root->left->left && !root->left->right) { // 左子树就是一个左叶子的情况
            leftValue = root->left->val;
        }
        int rightValue = sumOfLeftLeaves(root->right);  // 右

        int sum = leftValue + rightValue;               // 中
        return sum;
    }
};