A Swap Relaxation-Based Local Search for the Latin Square Completion Problem

Zhenxuan Xie, Zhipeng Lü, Zhouxing Su, Chu-Min Li, Junwen Ding, Yuxuan Wang

摘要

拉丁方阵补全（LSC）问题的目标是将 n 个符号分配到一个部分填充的拉丁方阵的空单元格中，使得每行和每列中每个符号恰好出现一次。本文提出了一种基于交换松弛的快速局部搜索算法，称为 SRLS，用于解决 LSC 问题。首先，它引入了一种新的搜索空间定义，禁止行冲突，并基于此定义了一个基于交换的邻域。其次，在基于交换的邻域中采用了一种颜色域松弛技术，通过临时接受某些约束的违规来连接高质量解。第三，采用了两个有效的评分函数来选择邻域操作，这些评分函数旨在最小化冲突边的数量以及颜色域违规的数量。最后，SRLS 使用了一种自适应重启机制，以平衡搜索的利用与探索。

在 1819 个公共基准实例上的大量实验表明，SRLS 在成功率和计算效率方面均优于文献中的最新算法。

1 引言

设 n 为一个正整数。阶数为 n 的拉丁方阵是一个 n \times n 的单元格网格，其中每个单元格被填充一个符号（从 1 到 n），使得每个符号在每行和每列中恰好出现一次。给定一个 n \times n 的网格，其中一些单元格已填充符号，而其他单元格为空。阶数为 n 的拉丁方阵补全（LSC）问题的任务是为每个空单元格填充一个符号，以形成一个拉丁方阵。

拉丁方阵补全（LSC）问题最早由 Hall [1948] 和 Ryser [1951] 提出。作为一个经典的 NP 完全问题 [Colbourn, 1984]，LSC 问题除了在理论上具有重要意义外，还在多个领域中有广泛的应用，例如光网络 [Barry and Humblet, 1993]、调度 [Kumar et al., 1999]、纠错码 [Colbourn et al., 2004] 以及组合设计 [Lovász et al., 2003; Colbourn and Dinitz, 2007] 等。

作为一个具有挑战性的组合优化问题，LSC 在最近几十年吸引了学术界的广泛关注。其中，已经提出了若干精确算法：Gomes 和 Shmoys [2002] 提出了三种求解 LSC 问题的完整方法，分别将该问题编码为约束满足问题（CSP）形式、混合线性规划/CSP 形式以及布尔可满足性问题（SAT）形式。此外，Ansótegui 等人 [2004] 系统性地比较了 LSC 问题的 SAT 和 CSP 模型。

除了精确算法外，还提出了多种元启发式算法，用于在合理的时间内为大规模实例找到高质量解。Haraguchi [2016] 提出了四种带有不同邻域的有效迭代局部搜索算法。Jin 和 Hao [2019] 提出了一种基于种群的记忆遗传算法 MMCOL，该算法通过将 n \times n 的单元格网格转换为一个具有域约束的拉丁方阵图来解决 LSC 问题。Pan 等人 [2022] 提出了一种名为 FastLSC 的快速局部搜索算法，该算法基于约简推理技术、新的冲突值选择启发式方法以及历史信息扰动机制，将 LSC 问题建模为一个图着色问题。根据我们所知，FastLSC 在性能上显著优于其他元启发式算法。然而，在一些非常困难的实例上，其成功率仍有改进空间。

在本文中，我们同样将 LSC 问题视为图着色问题，但直接利用其特定特性进行求解。具体而言，我们提出了一种基于交换松弛的局部搜索算法（SRLS），其结合了新的搜索空间定义、基于交换松弛的邻域、两个评分函数和自适应重启机制。SRLS 的一个关键特性是其搜索空间显著小于 MMCOL 和 FastLSC 的搜索空间。

我们的主要贡献可以总结如下：

1. 我们提出了两种新的约简规则来缩小颜色域，这些规则在效果上优于现有规则。
2. 我们引入了一种新的搜索空间定义，要求每个符号在每一行中恰好出现一次。基于此限制的搜索空间，我们定义了一种基于交换的邻域，该邻域通过交换同一行中两个单元格的符号，始终保持每行无冲突。
3. 通过引入颜色域松弛技术，我们扩展了基于交换的邻域的搜索空间，使得搜索能够通过带有颜色域违规的解轻松连接到高质量解。此外，我们采用了两个有效的评分函数，用于选择具有即时和潜在影响的邻域解，同时优化冲突边的数量和颜色域违规的数量。
4. 我们提出了一种机制，当当前解的质量相对较差时，从已找到的最优解重新开始局部搜索。此外，用于判断解质量是否相对较差的阈值会随着局部搜索的进行自适应更新，从而平衡搜索的利用与探索。
5. 在文献中广泛使用的 1819 个公共基准实例上测试表明，所提出的 SRLS 在成功率和计算效率方面，在所有测试实例中均优于最新的算法。
6. 我们进行了消融实验，以验证 SRLS 算法关键组件的优点，包括颜色域松弛技术、次要评分函数和自适应重启机制。

2 初步知识

阶数为 n 的部分拉丁方 L_p 可以与一个所谓的拉丁方图 G = (V, E) [Jin 和 Hao, 2019] 关联，其中：

• V = \{v_{ij} \mid 1 \leq i \leq n, 1 \leq j \leq n\} 是所有单元格的集合，v_{ij} 表示第 i 行第 j 列的单元格；
• E 是边集，其中 (u, v) \in E 当且仅当单元格 u 和 v 位于同一行或同一列。

显然，|V| = n^2 且 |E| = n^2(n-1)，因为每一行或每一列有 n(n-1)/2 条边。

第 k 行的单元格集合记为 RV_k = \{v_{k j} \mid 1 \leq j \leq n\}，第 k 列的单元格集合记为 CV_k = \{v_{i k} \mid 1 \leq i \leq n\}。

拉丁方完成（LSC）问题本质上是定义在上述拉丁方图 G = (V, E) 上的图着色问题，其中拉丁方中的符号被视为 G 的颜色。令 D(v) 表示图中单元格 v 的颜色域。如果单元格 v 填充了符号 k (1 \leq k \leq n)，则颜色域 D(v) 是单值域 \{k\}；而每个未填充的单元格 u 的（初始）颜色域为 D(u) = \{1, \ldots, n\}。

LSC 问题的目标是找到一个颜色映射 C : V \to \{1, \ldots, n\}，使得对于所有 v \in V，C(v) \in D(v)，并且对于每条边 (u, v) \in E，C(v) \neq C(u)。这实际上是一个预着色扩展问题的特例 [Biró 等人, 1992]。

对于任意 (u, v) \in E，如果 C(u) = C(v)，则称 u 和 v 为冲突单元格，(u, v) 为冲突边。解 C 的冲突边集合记为 CE(C)。解的质量通过 |CE(C)| 来评估。对于冲突边 (u, v)，如果 u 和 v 位于同一行，则 (u, v) 称为行冲突；否则，(u, v) 称为列冲突。

若某个单元格 v 被赋予的颜色不在其颜色域内，即 C(v) \notin D(v)，则称之为颜色域违规。DV(C) 表示导致解 C 出现颜色域违规的单元格集合。

基于上述符号表示，放宽约束后的 LSC 问题可以表述为如下形式：

目标 (1) 旨在最小化冲突边的数量。显然，原始 LSC 问题的一个可行解必须是该模型的最优解，即 |CE(C)| = 0。约束 (2) 规定每个单元格的颜色必须从其颜色域中选择。因此，LSC 问题从一个约束满足问题（CSP）转化为一个优化问题。

3 基于交换松弛的局部搜索

拉丁方阵是一个无行冲突或列冲突的 n-着色。因此，如果我们始终保持解无行冲突，并且仅通过交换同一行中两个单元格的颜色来修改解，LSC 问题就被简化为仅消除列冲突，从而大大限制了搜索空间。

在本研究中，我们提出了一种基于交换松弛的局部搜索算法，称为 SRLS，用于解决 LSC 问题。SRLS 采用了限制搜索空间的方法，这与以往算法显著不同。以往算法在每次迭代中通过将一个单元格的颜色更改为另一种颜色来同时消除行冲突和列冲突。接下来，我们将首先介绍 SRLS 的主要框架，然后详细描述其关键组成部分。

3.1 所提出的 SRLS 算法的主要框架

所提出的 SRLS 算法的主要框架在算法 1 中给出。SRLS 的一个显著特征是它始终禁止行冲突。因此，每种颜色在每一行中仅出现一次，使得每种颜色的单元格数量恰好为 n。算法的核心目标是消除现有的列冲突。通过使用有限的搜索空间，可以定义一个基于交换的邻域，专门用于解决列冲突。通过缩小搜索空间，可以更有效、更有针对性地解决这一问题。

SRLS 首先应用两种新提出的约简规则来简化问题实例，并随机生成一个无行冲突的初始解（第 1 行）。随后，通过局部搜索过程迭代地改进该解（第 3-11 行）。在每次迭代中，算法首先评估当前解的邻域，并根据两个评分函数和禁忌策略选择最优移动（第 4 行）。然后，算法对当前解执行该最优移动（第 5 行）。之后，如果当前解 C 是一个合法的拉丁方阵，即 |\text{CE}(C)| = 0，则返回当前解（第 6-7 行）。否则，将当前解 C 的质量与迄今为止找到的最优解 C^* 进行比较（第 8-11 行）。如果 C 不劣于 C^*，即 |\text{CE}(C)| \leq |\text{CE}(C^*)|，则用 C 替换 C^*（第 8-9 行）。否则，如果需要，局部搜索会自适应地从最优解重新开始（第 10-11 行）。最后，一旦经过的时间超过设定的时间限制，SRLS 会终止并返回最优解 C^*（第 12 行）。

3.2 初始化

我们提出了两种约简规则，用于缩小某些单元格的颜色域。需要注意的是，如果某个单元格的颜色域被缩小到一个单一值，该单元格的颜色就被固定。

约简规则 1：设 SV 为某一行（列）中的一组单元格，且 DS = \bigcup_{v \in SV} D(v)。如果 |DS| = |SV|，那么 DS 中的颜色不能用于为同一行（列）中的其他单元格着色，且应从这些单元格的颜色域中移除。

约简规则 2：设 SV 为某一行（列）中的一组单元格，CS 为一组颜色。如果 |CS| = |SV|，且 CS 中的颜色只能用于为 SV 中的单元格着色，不能用于为同一行（列）中的其他单元格着色，那么 CS 之外的颜色应从 SV 中每个单元格的颜色域中移除。

需要注意的是，MMCOL [2019] 和 FastLSC [2022] 中提出的三种约简规则是我们规则在 |SV| = 1 情况下的特例。

规则 1 和规则 2 可以通过调用约束规划求解器（如具有全异约束的 Choco [Prud’homme 等人, 2019]）来实现。我们构建了一个包含 2n 个全异约束的模型，并反复传播这些约束，直到没有更多单元格的颜色可以被固定为止。实验表明，与之前的约简规则相比，我们的约简规则可以缩小更多的颜色域，并修复更多的单元格。

设 RC_i (i = 1, \dots, n) 表示一组颜色，称为行冲突自由颜色，其定义为：用 RC_i 中的任意颜色为第 i 行的任意单元格着色，都不会导致行冲突。初始化过程如算法 2 所示。SRLS 反复应用全异约束传播器来更新颜色域，直到没有单元格的颜色能够被固定（第 5-8 行）。之后，SRLS 根据已固定颜色的单元格更新行冲突自由颜色（第 9-10 行）。然后，随机生成一个无行冲突的初始解（第 11-15 行）。具体来说，对于每个未着色的单元格 u_{ij}，使用行冲突自由颜色 RC_i 中的一个随机颜色 c 为其着色（第 14 行），并更新 RC_i（第 15 行）。最后，返回一个无行冲突的初始解（第 16 行）。

3.3 邻域结构与评估

为了改进初始解，我们采用了基于交换的邻域结构。用 m(u, v) 表示一个交换操作，通过交换同一行中未固定颜色的单元格 u 和 v 的颜色，生成一个邻近解 C \oplus m(u, v)。对于交换操作 m(u, v)，u 和 v 称为操作单元格。不同于以往文献中的策略（总是满足颜色域约束，即约束 (2)），我们在执行交换操作时放宽了这一约束。具体来说，对于操作 m(u, v)，即使 C(v) \notin D(u)（或 C(u) \notin D(v)），单元格 u（或 v）仍然可以被着色为 C(v)（或 C(u)。

需要注意的是，在我们的算法中放宽颜色域约束是至关重要的，因为它允许通过颜色域违规的解连接高质量解。带有颜色域松弛的问题可以被表述为如下形式：

需要注意的是，约束 (6) 明确规定始终禁止行冲突。

邻域评估是基于轨迹的元启发式算法中最耗时的部分。对于采用最佳改进策略的典型局部搜索算法，它会在每次迭代中评估所有可行的操作，并执行最优操作以尽可能优化评分目标。如果评估整个邻域（即交换同一行中任意两个单元格的颜色），则可能会有 O(n^3) 个交换操作，这对于大规模实例而言是巨大的计算量。因此，为了减少邻域的规模并保留大多数高质量的邻近解，我们只评估至少有一个操作单元格存在冲突的操作。

需要注意的是，仅对冲突单元格进行操作即可获得一个合法解，因为一个合法的拉丁方阵是与其关联的拉丁方阵图的 n-着色，没有冲突单元格。因此，如果当前解中颜色未固定且存在冲突的单元格数为 p，则邻域的规模将为 O(pn)，远小于 O(n^3)。

图 1 展示了基于松弛的交换操作的一个示例，包括一个阶数为 4 的部分拉丁方阵，其中有 4 个单元格已填充。单元格中的数字表示其颜色。三角形中的数字表示颜色已固定，而圆形中的数字表示这些单元格存在冲突，连接它们的边表示冲突的边。

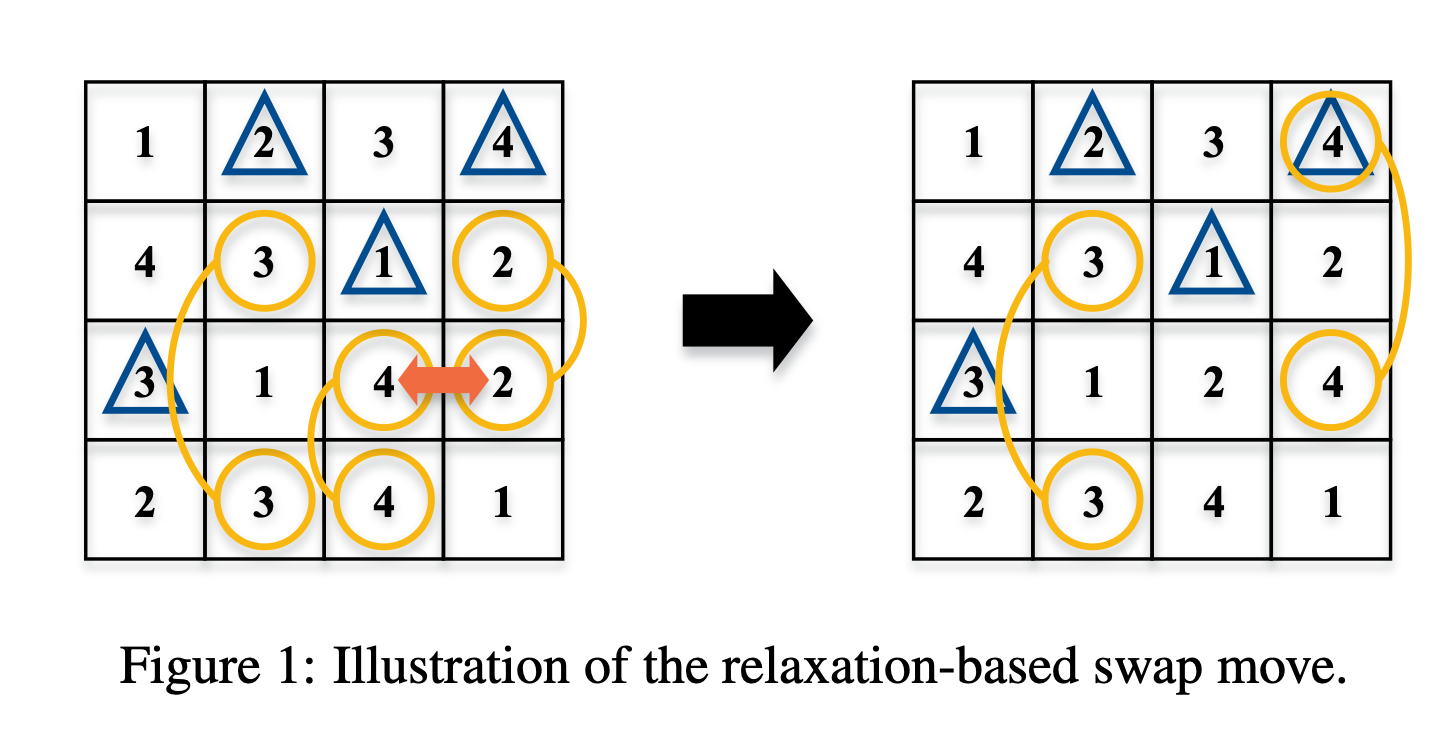
可以观察到，操作 m(v_{33}, v_{34}) 可以生成一个邻近解，从而减少一条冲突边。需要注意的是，由于单元格 v_{14} 的颜色已固定，此操作会导致颜色域违规，即 C(v_{34}) \notin D(v_{34})。

在局部搜索过程中，邻域评估是一个重要的组成部分。为了获得最优的邻近解并改进当前解 C，SRLS 使用了两个评分函数。由于冲突边的数量是优化目标，因此主要评分函数被定义为最小化冲突边的数量 |\text{CE}(C)|。对于产生邻近解 C' 的操作 m(u, v)，其评分如下定义：

为了区分具有相同主要评分函数值的多个交换操作，SRLS 引入了一个次要评分函数，该函数在搜索过程中起着重要作用。次要评分函数可以有效缓解梯度消失问题，并在许多局部搜索算法中引导搜索朝向一个有希望的方向 [Chen et al., 2021; Li et al., 2020; Zhang et al., 2022]。

对于单元格 v，如果其颜色域受到违规，即 C(v) \notin D(v)，这意味着单元格 v 与另一个颜色已固定的单元格存在冲突，无论剩余单元格的颜色如何选择，这都会导致一个非法解。对于两个具有相同冲突边数量的解，颜色域违规更少的解通常更容易修复为一个合法解。

因此，次要评分函数被定义为最小化颜色域违规的数量 |\text{DV}(C)|。具体来说，对于一个产生邻近解 C' 的操作 m(u, v)，次要评分函数的计算方式如下：

评分函数 \Delta f_1 和 \Delta f_2 的直觉在于：\Delta f_1 反映了操作的直接影响，而 \Delta f_2 可以被视为潜在影响。具体而言，在每次迭代中，SRLS 选择 \Delta f_1 值最小的操作，如果存在多个操作具有相同的 \Delta f_1 值，则选择 \Delta f_2 值最小的操作打破平局。如果 \Delta f_2 值仍然相同，则随机选择一个操作。

为了增强探索性，如果所有邻近解都会增加冲突边的数量（即 \Delta f_1 > 0），SRLS 会随机选择一个冲突单元格 v，并基于评分函数选择与 v 相关的最佳操作。

通过结合这两个评分函数，SRLS 不仅可以通过带有颜色域违规的解轻松连接到高质量解，还可以随着局部搜索的进行尽快最小化颜色域违规的数量。

3.4 禁忌搜索

在我们的局部搜索中采用了禁忌策略。禁忌搜索通常会使用基于最近性的禁忌表，以避免重新评估刚访问过的解 [Glover 和 Laguna, 1998]。对于禁忌表，当一个操作被执行后，该冲突单元格在接下来的 l 次迭代中被禁止重新着色为其原始颜色。具体来说，对于操作 m(u, v)，如果 u（或 v）是一个冲突单元格，则 (u, C(u))（或 (v, C(v))）被记录到禁忌表中。这里，禁忌期限 l 由以下公式确定：l = \alpha \cdot |\text{CE}(C)| + r(10)，其中 r(10) 是从 \{1, \dots, 10\} 中随机选取的一个数字 [Galinier 和 Hao, 1999]。

如果将一个单元格着色为另一个单元格的颜色在禁忌表中（即 (u, C(v)) 或 (v, C(u)) 在禁忌表中），则操作 m(u, v) 被声明为禁忌操作。此外，我们采用了一个简单的允许条件：即使某个操作被禁忌，但如果它能产生一个优于当前最优解的解，则允许选择该操作。

需要注意的是，我们基于前面提到的两个评分函数同时选择最佳禁忌操作和最佳非禁忌操作。在每次迭代中，只有当最佳禁忌操作优于最佳非禁忌操作且能产生一个冲突边数量小于当前最优解的解时，才会选择最佳禁忌操作作为最终操作。否则，选择最佳非禁忌操作。

3.5 自适应重启机制

与经典图着色问题 [Garey 和 Johnson, 1979] 不同，由于 LSC 问题的解中某些单元格的颜色已被固定，其对称性较弱。因此，LSC 问题比经典图着色问题更难摆脱差解陷阱。重启机制通常可以帮助搜索打破这种困境 [Lü 和 Hao, 2012; Wu 和 Hao, 2013]。因此，当解的质量足够差时，我们采用自适应重启机制，通过从迄今为止找到的最优解重新开始搜索来强化搜索过程。

算法 3 实现了这种自适应重启机制，使用了三个参数 rt_0、rt_{\text{ub}} 和 \text{accu}_{\text{ub}}。该机制的核心是一个重启阈值 rt。当当前解 C 和迄今为止找到的最优解 C^* 之间的冲突边数量的差距超过 rt 时，SRLS 放弃 C 并从 C^* 重新开始局部搜索（第 2-3 行）。同时，在重启后禁忌表将被清空。

为了平衡搜索的利用和探索，rt 初始化为一个较小的值 rt_0，并在每经历 \text{accu}_{\text{ub}} 次未超过 rt_{\text{ub}} 的重启后增加 1，以减少从 C^* 重启的频率（第 4-10 行）。